10.1 どの分類モデルを選ぶべきか

分類問題をあつかう学習器は特に分類モデルまたは分類器 (classifier) と呼ばれます. 分類モデルは, 連続的な数量ではなく, 0 または 1 のような離散的な変数や, 数値ではなくラベルで表されるカテゴリカル変数をラベル変数とします. 今回のインターンで使うのは最も単純な2値分類ですので, これを中心に説明し, マルチクラスやマルチラベル分類は今回は扱いません. これ以降は, いくつかの代表的な分類モデルの特性を紹介し, どのような場面で有効で, どのような場面でそうでないかのヒントを与えます.

10.1.1 分類モデルの数学的な定式化

ここでは, 機械学習の文脈で分類器を定式化します. まず目的変数 \(y\) を, \(1\) または \(-1\) の2値に揃えます34. この値はクラスと呼びます. 分類器は, クラスのいずれかの値を出力するため,

\[ f(\boldsymbol{x}_{i}):= \begin{cases} 1 & \text{if }g(\boldsymbol{x}_{i})\geq0\\ -1 & \text{if }g(\boldsymbol{x}_{i})<0 \end{cases} \] と定義されます. \(g(\boldsymbol{x}_{i})\) がゼロ以上なら\(1\)を, 未満なら\(-1\) を出力する, という条件づけを行います35. \(g(\boldsymbol{x}_{i})\) は判別関数 (discrimination function) とか識別関数とか呼ばれます. 識別関数はロジスティック回帰のように分類される確率を出力するものもあれば, 1を超えたりマイナスになったりと必ずしも確率を出力するとは限らないものもありますが, 当てはめたいデータの目的変数は2通りの値しかありません.

そのため, 回帰のように残差でモデルの当てはまりを評価することはできません. 単純に, 予測値が的中すればゼロ, ハズレれば1の損失がある場合を考えてみましょう. これを 0/1損失といいます.

\[ l(\theta):= \begin{cases} 0 & \text{if }y=f(x)\\ 1 & \text{if }y\neq f(x) \end{cases} = 1(\mathrm{sign}(g(x)y)\neq y) \]

ここで, \(\mathrm{sign}(\cdot)\) は入力した数値の符号を返す関数で, 正なら\(1\)を, 負なら\(-1\) を返します. \(1(\cdot)\) は指示関数といい, カッコ内の条件が真なら1を, そうでないならゼロを返す関数です. 以上から, 2値分類モデルは0/1損失の最小化問題を解けば良いように見えます.

\[ \min_{\boldsymbol{\theta}}\sum_{i=1}^{n}\mathrm{sign}(g(x_{i})y_{i}) \]

この式はつまり, 分類モデルの誤りが多いほど, 0/1損失が増大するため, 損失が最も小さくなるようなパラメータ \(\boldsymbol{\theta}\)を選ぶことで最善のモデルが得られるというアイディアを意味します.

しかし, これは微分できない損失関数を扱うことになります. 微分できない関数の最小化問題を解くのは一般に難しいです. 特に0/1損失では, いくつかの解候補から最適なものを探す組合せ最適化問題であり, その候補は \(2^{n}\) 通りになるため, アルゴリズムで探索するのは現実的に困難です. そこで, 最小化問題として扱いやすく, かつ0/1損失に近い性質をもつ関数を代用の損失関数とすることがほとんどです.

では, どのような「代理の」損失関数を用いるのが適しているのでしょうか. 0/1 損失は, \(g(x)y\) がゼロを超えるかどうかで損失の大きさが決まります. これをマージンといい, \(m=g(x)y\) と表すことにします. すると, 観測点 \((x_{i},y_{i})\) に対して予測器が正しく分類するとき, マージンは \(m\geq0\) となり, 逆に分類を誤ったときは \(m<0\) となります. さらに, \(y\in\{-1,1\}\) なので, \(y-m\) を残差とすれば, 最小二乗法と同様に二乗損失を適用できそうです. \(y^{2}=1, 1/y=y\) であることに注意すると, 二乗損失は

\[\begin{align} \left(y-m\right)^{2} &= y^{2}\left(1-m/y\right)^{2} \\ &= \left(1-m\right)^{2} \end{align}\]

となります. よって, 二乗損失関数を分類問題に適用すると, 0/1損失とは異なり, \(m=1\) のときに損失が最小となり, \(m>1\) のときに, 正しく分類できるにもかかわらず損失を発生させてしまいます ([fig:ml-loss-class]).

分類問題では, 実用的な損失関数として, \(m>0\) のときに損失が発生しないか, 損失を小さく抑えられるような関数を使うのがより望ましいです. 具体的には, ヒンジ (hinge, 蝶番) 損失, ロジスティック損失 (対数損失), 指数損失などがよく用いられます. 分類器の多くは損失関数の違いで特徴づけられ, ヒンジ損失はサポートベクターマシン (SVM) に, ロジスティック損失はロジスティック回帰36 に対応します (図 10.1).

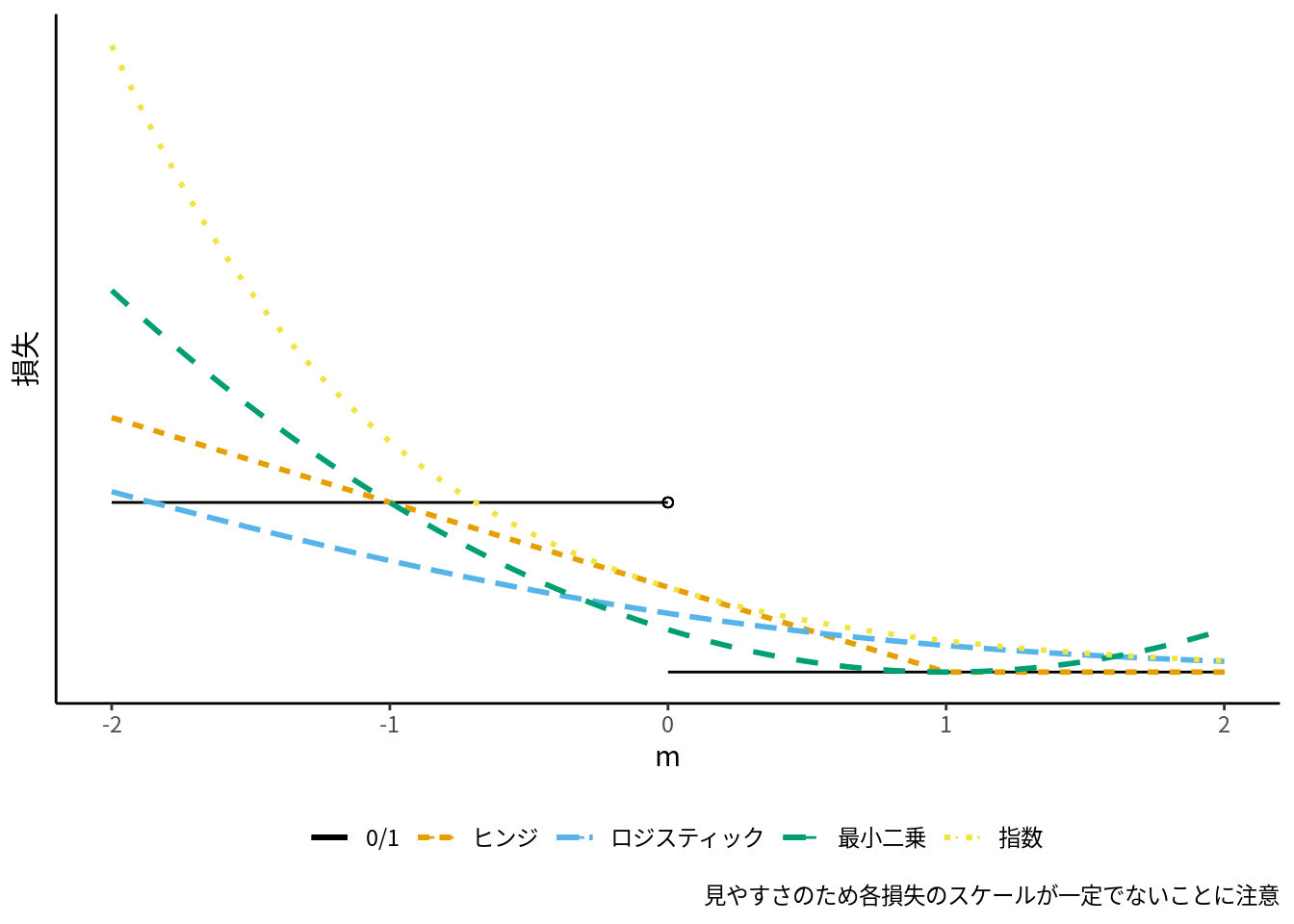
主な分類器の損失関数

図 10.1: 主な分類器の損失関数

10.1.2 ロジスティック回帰37

ロジスティック回帰の損失は, マージン \(m_i\) を使って以下のように定義できます.

\[ l_{i}:= \ln(1+\exp(-m_{i})) \]

これをグラフで表すと, マージンに対して減少し \(m>0\) でゼロに近づきます. よって, 0/1 損失で述べたように, \(y_{i}=1\) のときに損失が発生しにくい損失です. \(m\) を使わずに表すと, ロジスティック回帰は以下のような損失関数の最小化問題を解くことになります.

\[ \min_{\boldsymbol{\theta}}\sum_{i}l_{i}= \min_{\boldsymbol{\theta}}\sum_{i}\ln(1+\exp(-g(\boldsymbol{x}_{i})y_{i})) \]

ロジスティック回帰の識別関数は, 特徴量に対して線形な関数 \(g(\boldsymbol{x}):= \boldsymbol{x}_{i}^{\intercal}\boldsymbol{\theta}\) です. このため, ロジスティック回帰は線形分類器と呼ばれるタイプの分類器です. 線形分類器とは具体的にどういうことでしょうか? 2次元の特徴量に対して, 分類の境界線, 決定境界 (decision boundary) や決定領域 (decision region) がどこにあるかを描くことで特性がはっきりします. x1, x2 という特徴量を散布図で表し, それを学習した結果の決定領域/境界を重ねてみます.

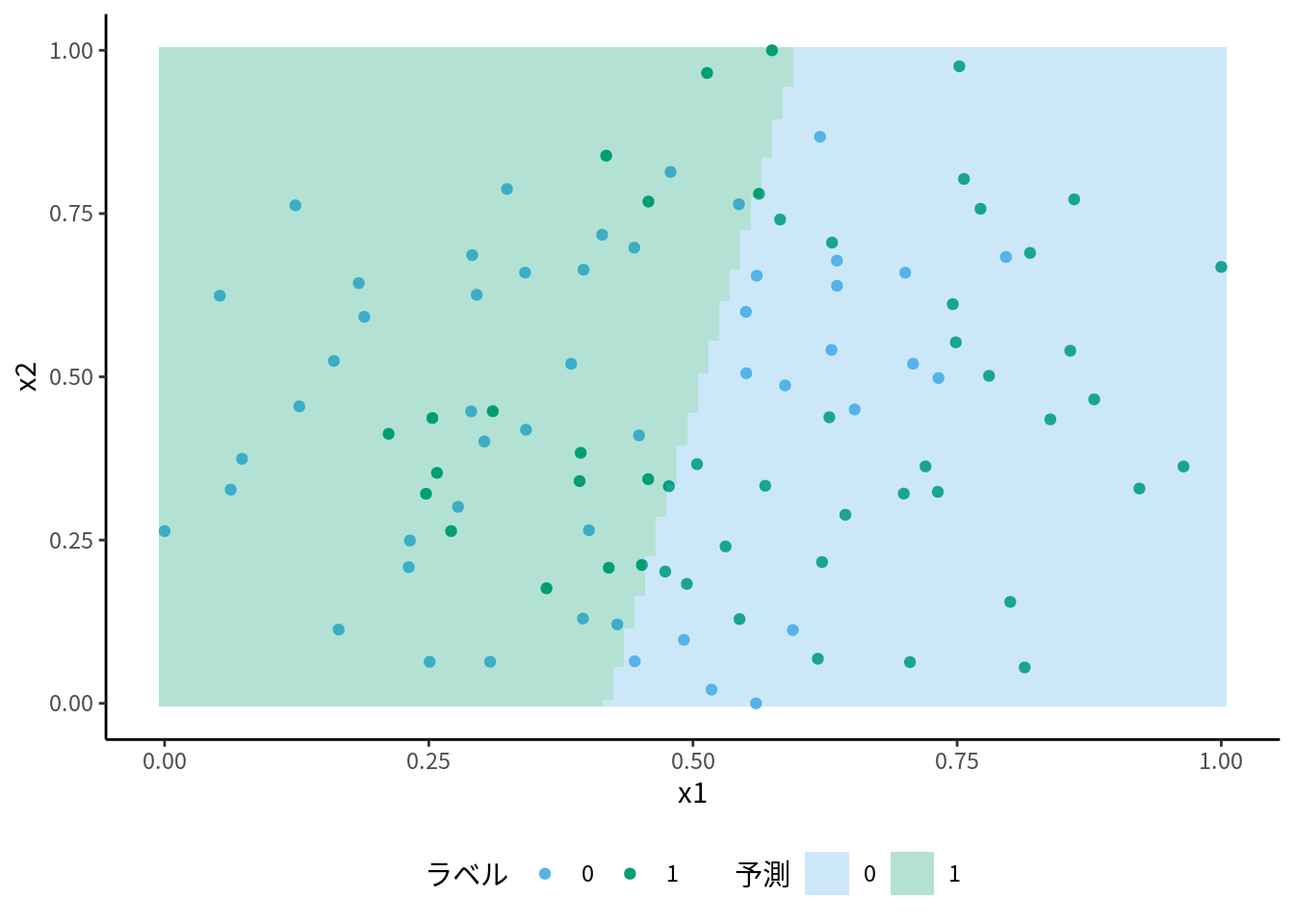
ロジスティック回帰の決定境界

図 10.2: ロジスティック回帰の決定境界

このように, ロジスティック回帰の決定境界は直線となります. これはロジスティック回帰が, 正例・負例の集合が直線 or 平面で完全な決定境界を引ける分布である, 数学で言う互いに線形分離可能 (linearly separatable)だと前提していることを意味します. そして今回, 散布図に見られるデータの分布は, どのような直線でも正例と負例を分けることができません.

しかしながら応用においては今回のタスクのように2次元以上の特徴量を扱うことがほとんどなので, 散布図を書いて扱うデータが線形分離可能なのかどうかを確認することは難しいです (もちろん, 訓練データのみで確認できたことがその外部でも同じように言えるのかという問題もあります). よって, ロジスティック回帰を使うのが適切なのかは断片的な情報から推理するしかありません. むしろ逆に, ロジスティック回帰モデルによる当てはまりがとても悪い場合, 実際の決定境界が複雑な形状をしているかもしれない, という新しい仮説を生むきっかけになりえます.

ロジスティック回帰は計算が不可能なケースがいくつかあります. 例えば正例と負例の2値分類なのに, どちらか片方しかないケースです38. これは当たり前なのでわかりやすいですが, 見落としがちなエラーとして, 完全分離可能 (complete separatable) または準完全分離可能 (quasi-complete separatable) なデータである場合も計算ができないことがあります. 完全分離可能な特徴量行列とは, 全ての特徴量が, それぞれ適当なしきい値だけでラベル変数を完全に分類できてしまうことです (Albert and Anderson (1984)).

\[ y_i=1 \Leftrightarrow \boldsymbol{\theta}^\top \boldsymbol{x}_i > 0 \forall i \]

完全分離可能なデータの例は表 10.1 のようなものです. このデータでは, \(x \leq 3\) であることと \(y = 1\) が対応しています.

表 10.1: 完全分離可能なデータの例
x y
1 1
2 1
3 1
4 0
5 0
6 0

さらに準完全分離可能というのは, 2種類の特徴量の関係で \(y\) を完全に予測できるデータのことを指します. 表 10.2 は, \(x1 \leq 3\) では \(y\) を正確に予測できませんが, \(x1 > x2\) という条件で \(y\) を完全に予測できます.

表 10.2: 準完全分離可能なデータの例
x1 x2 y
1 2 0
2 3 0
3 1 1
4 4 0
5 5 0
6 6 0

これらの例はやや極端なので, 実際にこんなデータに出くわすことはないと思われるかもしれません. しかし, 特徴量の種類が膨大だったり, CTR 予測のように極端に正例 (負例) が少ないケースでは, (準) 完全分離であっても気づきにくいです. この問題は最尤推定でモデルを求めていることに起因します39. つまり, 正則化などを使って解決する必要があります.

10.1.3 ロジスティック回帰と正則化

過学習を防止する方法として, 正則化 (regularized) あるいは 罰則付き (penalized) 学習と呼ばれます. これは, 目的関数を損失関数に正則化(罰則)項を足したものにして学習することです. 正則化項は通常, \(L^p\) ノルムが使われます. つまり, 以下のような目的関数を最小化します.

\[\begin{align} L(\boldsymbol{\theta}) := \sum_{i=1}^N l_i(\boldsymbol{\theta}) + \lambda \left\Vert \boldsymbol{\theta} \right\Vert_p \tag{10.1} \end{align}\]

\(\lambda\) は正則化の大きさを決める非負のハイパーパラメータ40で, 学習では決定できません. \(p\) は計算の容易さから, 1または2が採用されます. \(p=1\) のケースを \(L_1\)正則化とか Lasso ロジスティック回帰といい, \(p=2\) のケースを \(L_2\) 正則化またはリッジ (ridge) ロジスティック回帰と言います. さらに, \(L_1\) 正則化項と \(L_2\) 正則化項の両方を追加したものを エラスティックネット (elastic net) と言います. 代表的な\(L^p\) ノルムの等高線を2次元上に描くと, 図 10.3 になります.

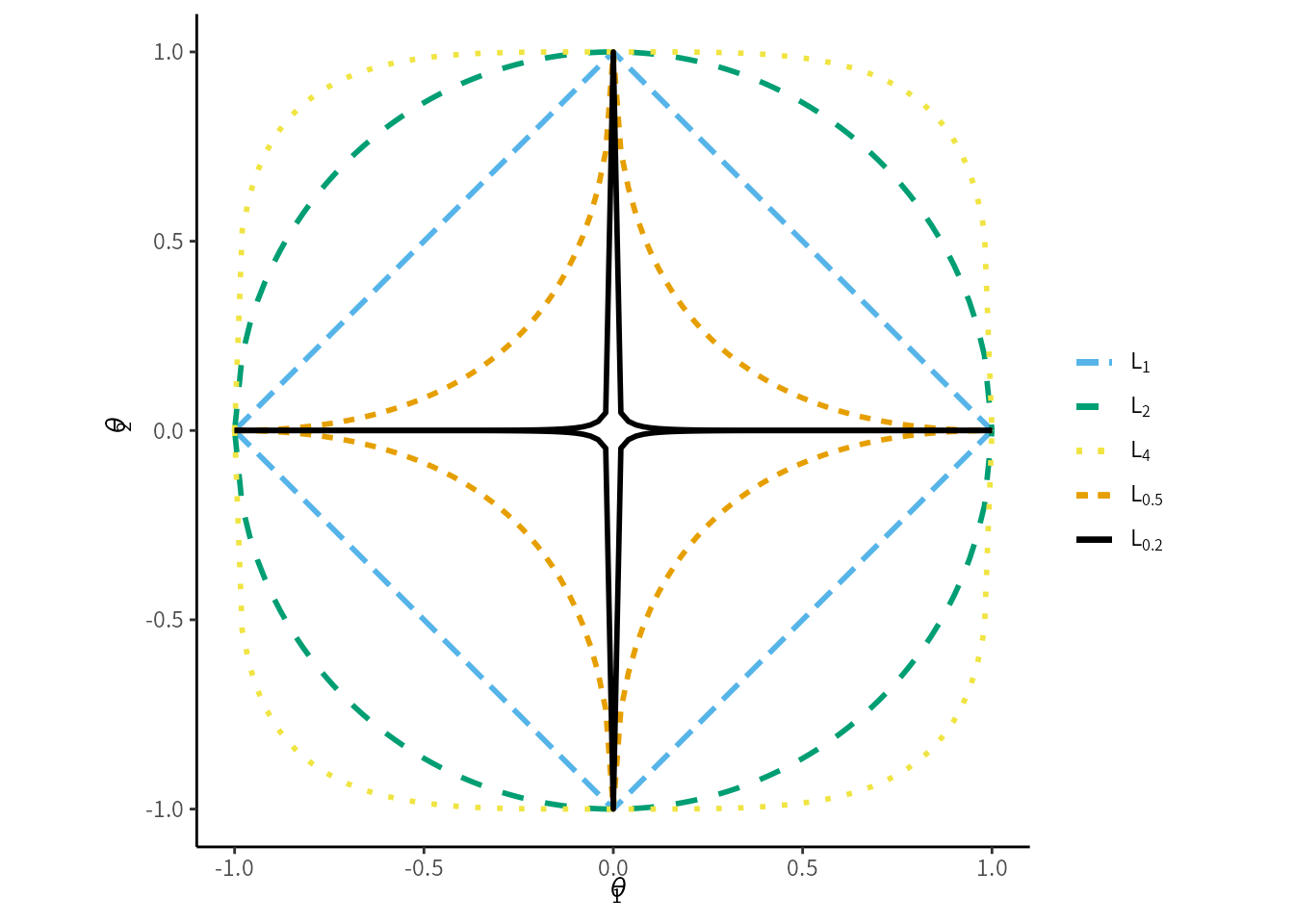
代表的なノルム

図 10.3: 代表的なノルム

ノルムがなんであれ, \(\boldsymbol{\theta}\) の絶対値が大きくなるほど正則化項の値は大きくなります. つまり, 正則化を使用すると, 全てのパラメータをゼロ方向に誘導する効果があります. そして特に \(L_1\) 正則化は各パラメータをゼロにするか, ほとんど縮小しないか, の両極端に比較的なりやすく, パラメータにゼロ要素が増える傾向があります. ここから, \(L_1\) 正則化を使う学習をスパース推定と呼ぶことがあります.

これはノルムと損失関数の等高線の接点をイメージするとわかりやすいでしょう.41 図10.4 は図 10.3 のように原点を中心とした正則化項のノルムに, 損失関数の等高線を重ねたものです. 青い楕円が損失関数の等高線であり, 中心点が最小値です. 正則化項がある場合, この最小値ではなくノルムの内側の範囲で最小の点を選ぶことになります. すると L1 ノルムでは, 図のようにいずれかのパラメータがゼロになる端点が選ばれやすいことが想像できると思います.42

図10.4 と同様の図は既存の多くの教科書でも掲載されていますが, いくつか注意が必要です.

  1. L1 正則化で, 常に端点が選ばれるとは限らない
    • 損失関数側の等高線を平行移動したものを想像してください
  2. 4次元以上のパラメータ空間の場合は想像しづらいかもしれませんが, 通常は 2, 3次元と同じように各パラメータがゼロに選ばれやすいと考えられます
    • 適切な推定となるかも含めて, パラメータの次元と特徴量の次元の大小関係も条件に関連してきます. 詳細が気になる方は, この章で紹介しているスパース推定に関する本を調べるとよいかもしれません.
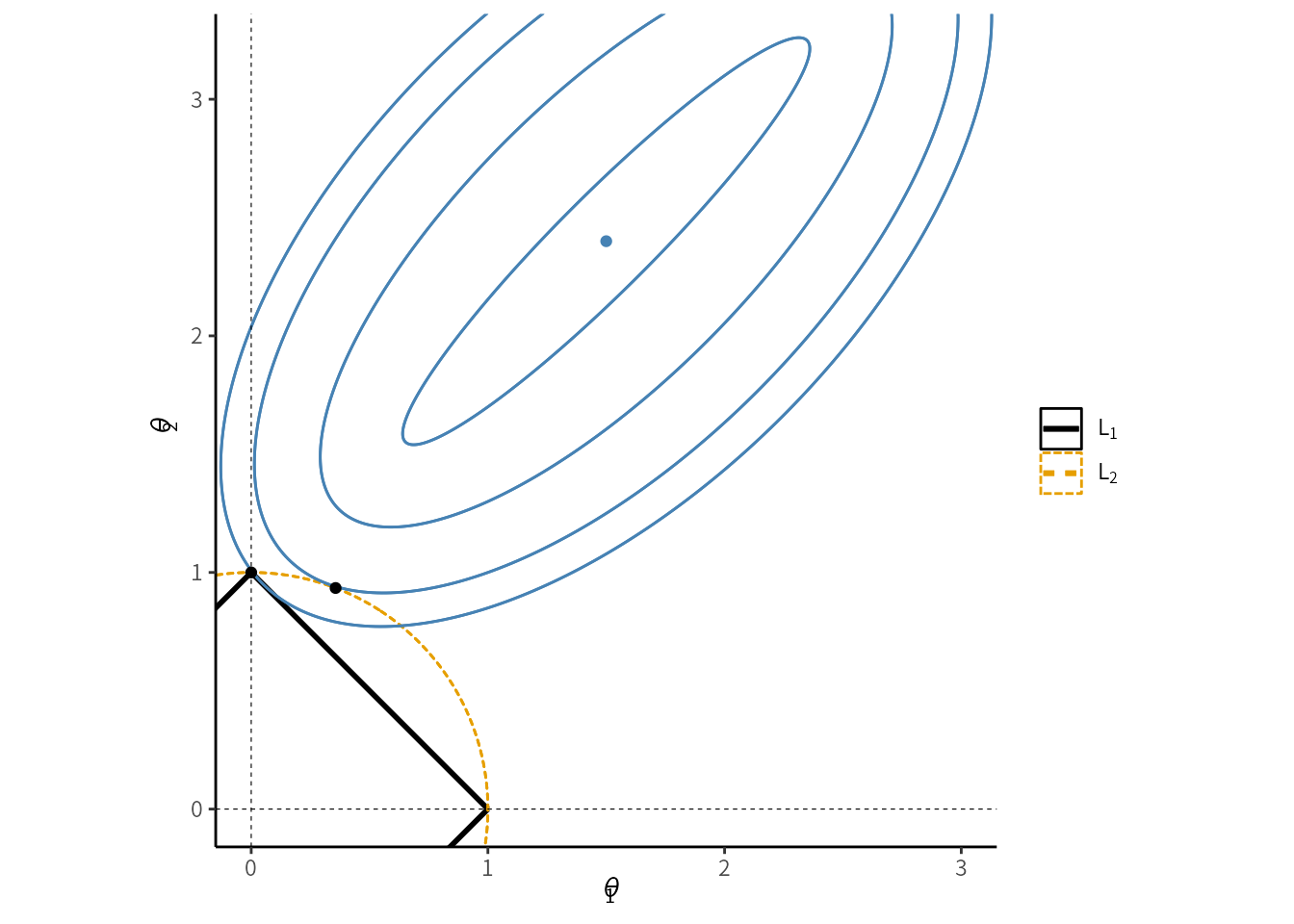
L1, L2 ノルムによって決まるパラメータの違い

図 10.4: L1, L2 ノルムによって決まるパラメータの違い

以下のような前提条件のもとで, ロジスティック回帰で \(L_1\) 正則化は効果的です.

  1. ラベルの比率が均等である, つまり,

\[ \mathrm{E} y_i = 0.5 \]

である.

  1. 全ての特徴量は, それぞれ期待値がゼロで, かつ分散が全て等しい \[\begin{align} \mathrm{E} x_d &= 0, \forall d=1,\cdots,D\\ \mathrm{V}(x_d) &= v, 0<v<\infty, \forall d \end{align}\]

  2. 特徴量どうしで相関がない

仮に全ての \(\boldsymbol{\theta}\) がゼロならば, 判別関数は \(\mathrm{E}g(x) = 0\) となり, これが\(y_i\) の期待値と一致するには, \(y_i\) の期待値のほうを調整しなければなりません. さらに, ここから特徴量のスケーリングが必要であることもわかります. また, 特徴量の期待値がゼロという仮定は正則化の際にはバイアス項を含んではならないことを意味する点にも注目してください43.

もしいくつかの特徴量どうしの相関がある場合, 特に \(L_1\) 正則化はそれらのうち1つだけしか選ばない傾向にあります. これに対処する方法として, (1) PCAで基底を取り直すなどの前処理を工夫することで対処する, (2) エラスティックネットを使用する, (3) グループLASSOといった構造的スパース学習と呼ばれるタイプの正則化を使う, といった方法があります. (2) のエラスティックネットは, グループ効果といい, 仮に変数間で相関があっても, 両者に同程度の正則化の効果が発生することが証明されています (Zou and Hastie 2005). (3) もまた, 変数間で相関のあるようなデータへの対処として考案されましたが, その多くは変数間の構造に関して興味がある場合に使われます. (1) (2) が scikit-learn に実装があるのに対し (3) の実装はありませんし, 計算が複雑になることが多いです.

正則化の計算について, \(L_2\) 正則化を追加しても目的関数が相変わらず滑らかな凹関数であるため, 準ニュートン法での計算が可能です. 一方で \(L_1\) 正則化を追加した場合はそうではないため, 他の最適化アルゴリズムによる計算が必要で, それらは多くの場合準ニュートン法より計算時間がかかります. (参考: セクション 10.2).

こういった正則化についてより詳しく知りたい場合, 富岡 (2015);川野, 松井, and 廣瀬 (2018) が取っ掛かりとして良いでしょう.

特徴量間の相関を確認する方法として, 正則化パラメータ \(\lambda\) に対して各パラメータの変化を折れ線グラフにするという方法があります (図10.5). 無相関ならば \(\lambda\) の増加に対して順調にゼロに近づくはずですが, 一時的にゼロから離れることがあるなら, いずれかの特徴量と相関している可能性があります. Scikit-learn の公式ドキュメント https://scikit-learn.org/stable/auto_examples/linear_model/plot_ridge_path.html にはサンプルコードが掲載されています.

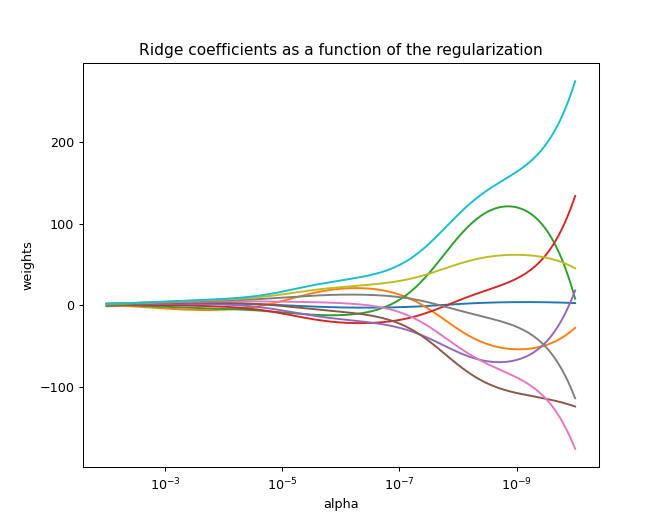
正則化パラメータとパラメータの関係のプロットの例

図 10.5: 正則化パラメータとパラメータの関係のプロットの例

10.1.4 決定木

決定木 (decision tree) はここまでで紹介したような損失関数の最小化問題とは発想が異なります. 特徴量A がゼロ以上なら1, ゼロ未満なら-1, といったように, 2択の条件分岐を繰り返すことで, 分類ルールを決定する方法です. これを木構造 (ツリーネットワーク) と言います. 図で見てみましょう. 最も簡単なのは, 特徴量を1つだけ選び, その特徴量があるしきい値以下かどうかだけで判定します. 10.6 は, 観測点が100件, x1, x2 という2つの特徴量のあるデータで学習した木構造です. x2 が 0.229 未満かどうかで判定しています. この分岐の発生してる点をノード (節) といいます. 特に図のように分岐の原点となっているノードを根 (root) ノードと呼びます. ノードは2つに分岐し, さらにそれぞれ2つのノードにつながっています. 分岐のことを枝 (edge) といいます. 根ノードから分岐した2つのノードには分岐がなく, 木構造の末端となっています. このようなノードを葉ノード (leaf node) といいます. 分岐が1つだけの決定木を特に決定株 (stamp) といいますが, 実用レベルではここまで単純なものを使う場面はほとんどありません.

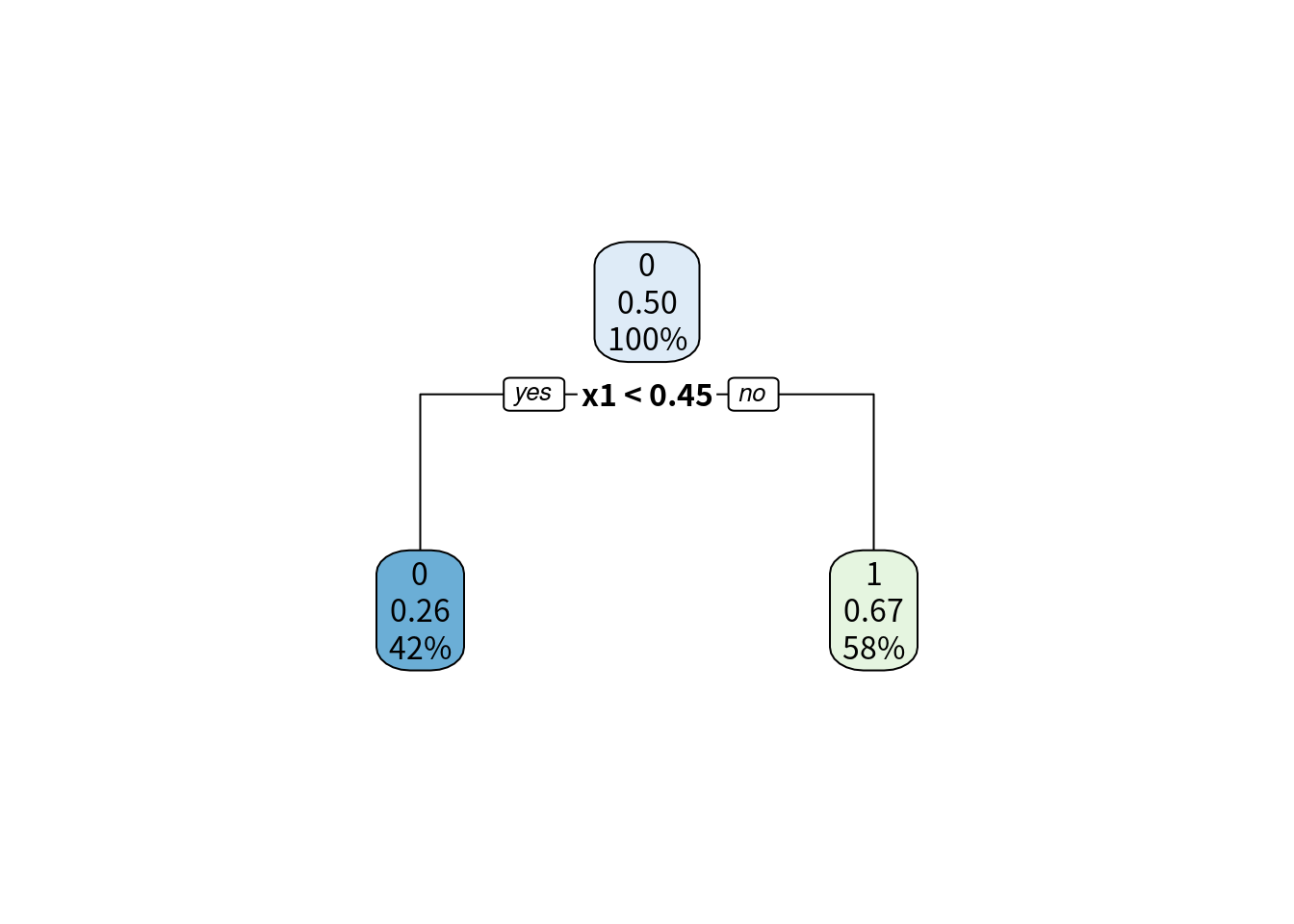
決定「株」の木構造

図 10.6: 決定「株」の木構造

決定株の葉ノードを見ると, 左は x1 が 0.45 未満という条件を満たすグループで, 0 と予測されますが, 実際には観測点の26%が 1 であり, 誤分類をしています. この決定株の決定領域が 図 10.7 です. \(x_{1}\leq 0.45\) という条件でしか判定していないので, 縦軸 x1 に垂直な線で分けられただけの非常に単純な分類ルールです. 決定株による分類では, まだいくらか誤分類があります. そこで, 決定株の葉ノードからさらに枝を派生させればもっと細かく分類でき, 誤分類が減るはずです. これが決定木です.

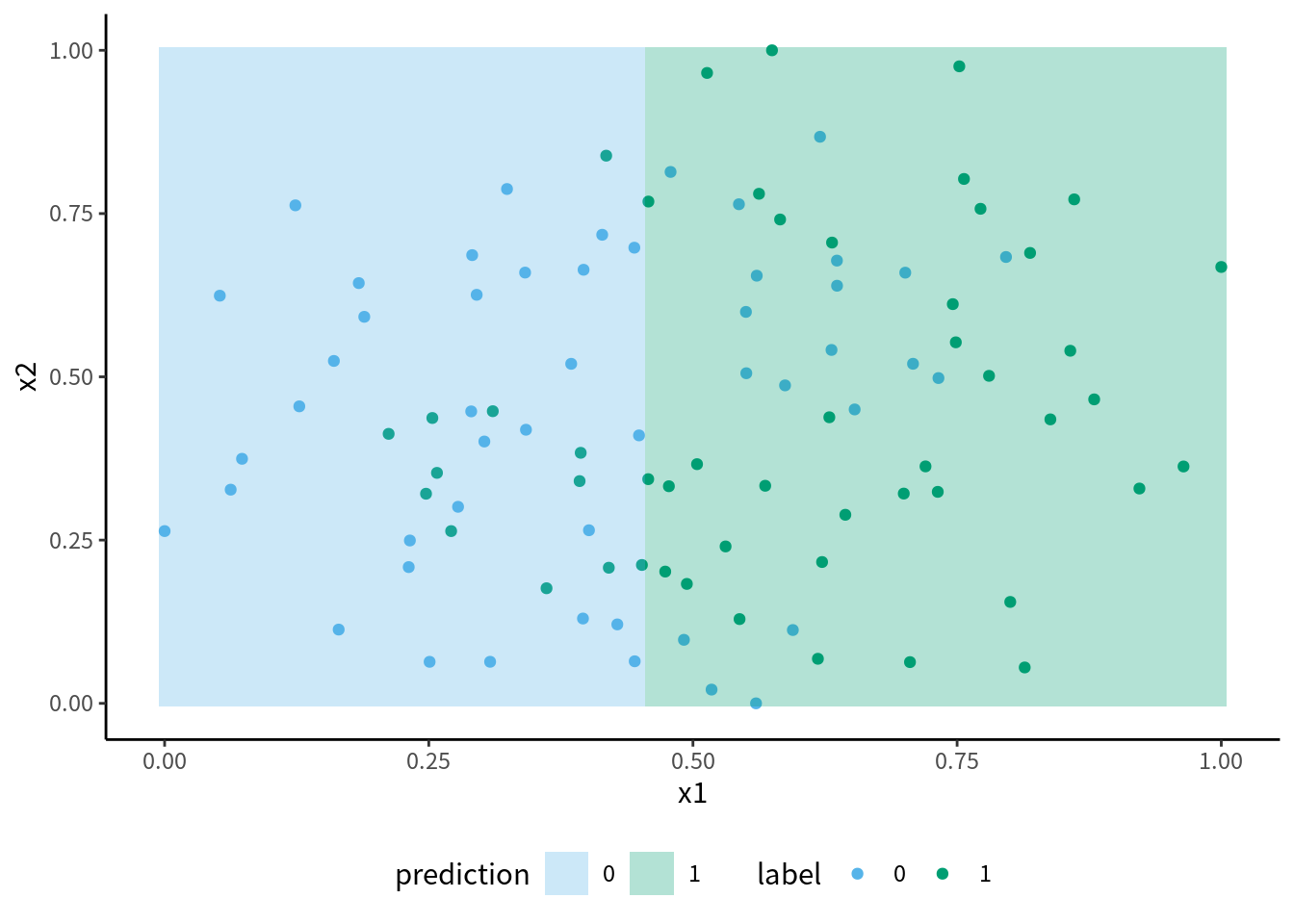
決定「株」の決定領域

図 10.7: 決定「株」の決定領域

枝を増やせばさらに誤分類が減ります. 同じデータでより枝を増やした決定木を学習させて得られた木構造が図 10.8 です. これを見ればわかるように, 決定木とは YES/NO の2択の質問を繰り返して正解に至るアルゴリズムと解釈できます. この決定木の決定境界は図 10.9で表されます. 1本の直線でしか分類できないロジスティック分類と違い, 決定木はより複雑な決定境界を形成し, 誤分類をしていません. この木構造をデータから学習するのが決定木のアルゴリズムです.

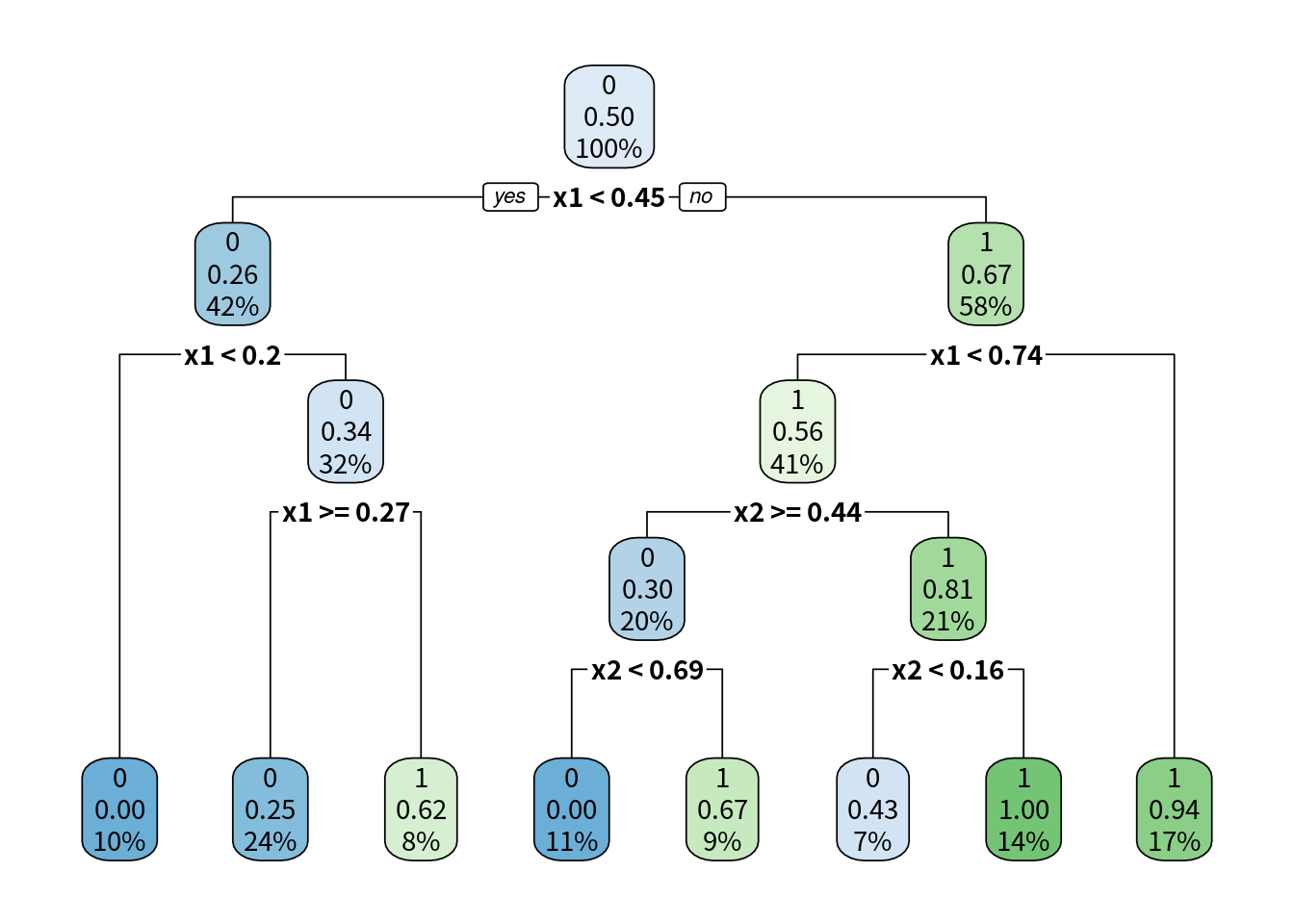
決定木の木構造

図 10.8: 決定木の木構造

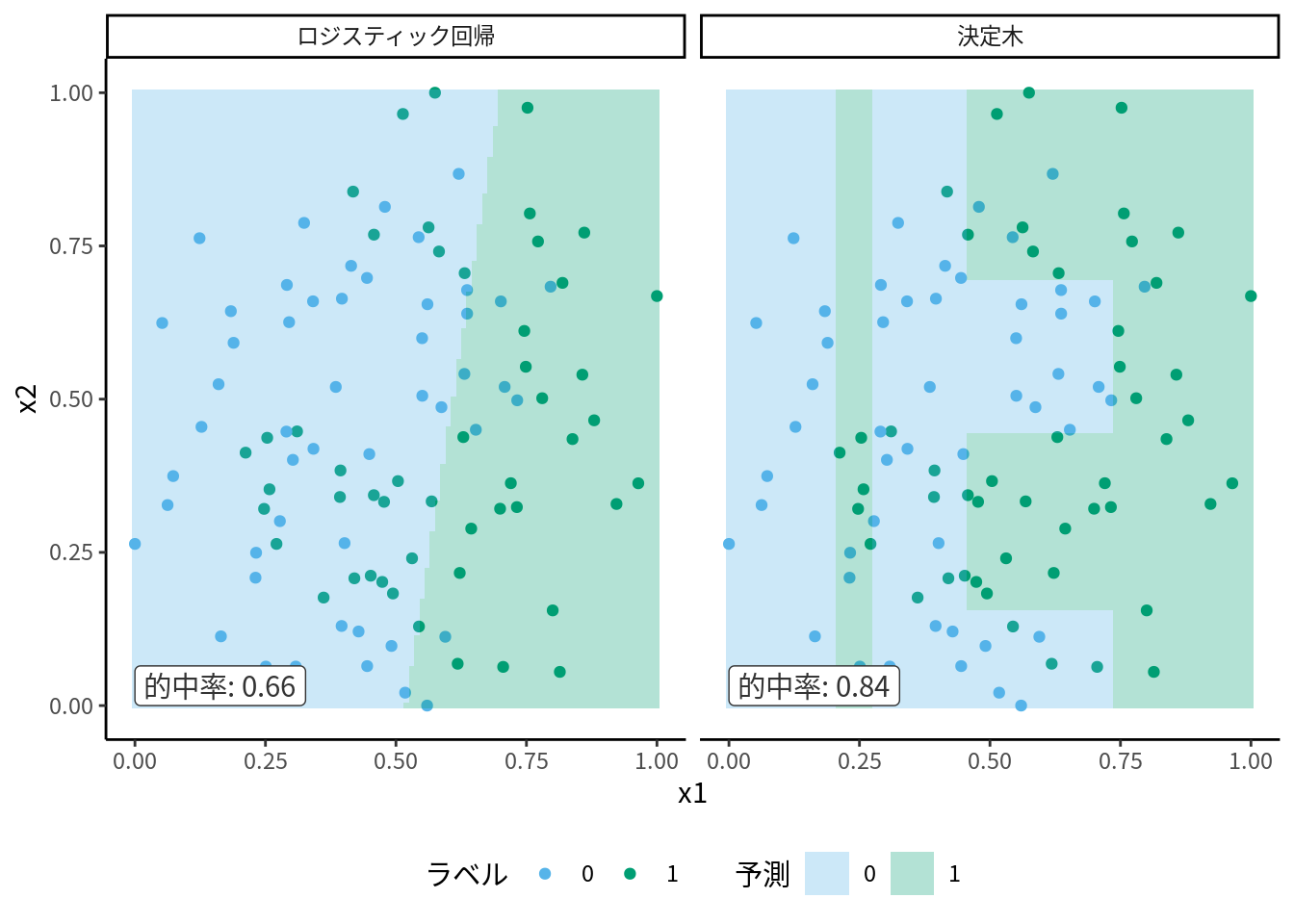
決定木とロジスティック回帰の決定領域

図 10.9: 決定木とロジスティック回帰の決定領域

では, この木構造をどうやればうまく決定できるかを説明します. 厳密には, 「決定木」とは特定のアルゴリズムではなく, 木構造を学習するいくつかのアルゴリズムやその実装の総称です. よく知られているものには, 古典的な CHID, ID3 ほか, 比較的最近 (?), 90年代に考案された C4.5 というものがありますが, ここでは一番広く普及している CART (classification and regression tree) を基準に説明します. CART アルゴリズムは, R言語の rpart パッケージや, Python の scikit-learn などいろいろなライブラリで採用されています.

木構造を決めるには, (1) どの特徴量が, (2) どういう値以下 (以上) か, という分岐の条件を決める必要があります. この条件は, 誤分類のあるノードから, 新たに枝を増やすとして, 最も誤分類を改善できるような特徴量のしきい値を選びます. この誤分類の大きさを, 不純度 (inpurity)といいます. 不純度はジニ多様性指数 (Gini diversity index) を計算し評価しますが, CART 以外の決定木アルゴリズムで使用される交差エントロピー (cross entropy, 情報ゲイン information gain, 逸脱度 deviance とも) でも評価できるオプションのある実装が多いです.

よって, 決定木はロジスティック分類や SVM のように全体の損失関数を最小化するのではなく, 分岐1つ1つで最適化を行うという点で, ヒューリスティックなアルゴリズムと言えますが, 際限なく分岐を増やすことで誤差の最小化を達成することができます.

ロジスティック回帰や SVM は, 基本的には線形回帰モデルと同様に, 特徴量に対する回帰係数 (=パラメータ)として与えることで, 各特徴量が予測値の決定にどの程度影響しているのか (偏相関係数) を知ることができました. しかし, 決定木のアルゴリズムでは, 回帰係数が存在しません. 代わりに, 特徴量の重要度 (importance) というものが用いられています.

では決定木による予測モデルはどのような形状になるのでしょうか? 決定木による分類は連続的な関数ではありません. そのため, 例えば欠損値を含む数量であっても, 補完することなく計算できます. さらに, 特徴量と分類の関係が線形ではなく非線形の関係にあっても分類できます. 図 10.9 を見れば, 決定木によって作られた識別の境界線は, 平面上に表すと格子状になり, ここからさらに分岐を多くすることで, 複雑な分類境界線であっても細かい格子状の境界線で近似して表現できることが想像できると思います. この点, ロジスティック回帰やSVMは, そのままでは直線的な分割しかできず, この図のように直線で分割できないようなデータの分類には向いていません. よって, 決定木のほうが非線形な構造にも当てはめられる, より自由度の高い学習アルゴリズムといえます.

決定木は計算リソースの許す限り分岐を際限なく増やし, 誤分類を減らすことができます. つまり, この格子状の分割をどんどん細かくすることができます. しかしそのような決定木は多くの場合過学習となります. そこで, 誤分類がなくなるまで分岐を増やすのではなく, 枝の深さに上限を課したり, 誤分類がゼロになるまで繰り返すのではなく, 誤分類が一定の許容量未満になった時点で枝の追加をやめる, といった方法がとられます. あるいは, 一旦は作成した分岐を削除する剪定 (plunning) と呼ばれる方法もあります. 決定木はヒューリスティックなアルゴリズムですが, このように学習を調整する手段がいくつもあるため最適化の調整が可能です. しかし調整の方法が豊富ということは, それだけ手順が複雑になります. 現在は決定木が考案された時代よりも計算機の性能が大きく向上しています. そのため, 単体の決定木でこれらのパラメータを調整して使うよりも, この後で紹介するアンサンブル学習の方法論を決定木に応用した, ランダムフォレスト (random forest) や 勾配ブースト木 (gradient boost decision tree), AdaBoost tree といった派生的な学習アルゴリズムが使われることが多いです. これらは木の単体の複雑さをどう調整するかとは別のアプローチで, 過学習を抑制することができます.

10.1.5 その他の基本的な分類器

教科書ではこれ以外にしばしば, ナイーブベイズ分類とサポートベクターマシン (SVM) が取り上げられます. 特にSVMは, モデルの誤差の推定に関する重要な理論であるヴァプニーク=チェルボネンキス次元 (VC次元) の説明によく使われます. これはモデルの誤差の理論上の上界を求めることができるとする理論ですが, 現実的には計算が困難です. SVM はこの計算が可能な分類器の1つですが, 一方で計算量の割に当てはまりの良いモデルを得ることが難しいため, 実用上はあまり使われることがありません. なお, モデルの誤差の評価に関してはこの後のセクションで詳しく紹介します.

10.1.6 アンサンブル学習

アンサンブル学習 (ensemble learning) あるいは集団学習とは, 複数の学習器の結果を統合して予測値を得る方法のことです. 分類問題ならば各学習器の予測値のうち, 最も多く予測されたラベルを選ぶ「多数決投票」を, 回帰問題ならば各学習器の予測値の平均値などを最終的な予測値として出力することが多いです. アンサンブル学習は大きく分けて, バギング (Bagging), スタッキング (Stacking), ブースティング (Boosting) の3種類があります.

アンサンブル学習では, 途中で作成する学習器を弱学習器 (weak learner, 基本/基底学習器と呼ばれることもある) と呼び, 最終的な出力を行う学習器をメタ学習器 (meta learner)44 と呼びます. 弱学習器とメタ学習器の組み合わせによる出力は, 適切に設定すれば弱学習器よりも精度のよい予測をするため, メタ学習器は強学習器 (strong learnear) とも呼びます. メタ学習器の典型的なものはモデル平均化 (model averaging) で45, 複数のモデルの結果の平均を計算します. ここでいう強弱というのは相対的な意味なので, 必ずしも弱学習器は性能の低いものでなければならないという決まりはありませんが, アンサンブル学習はいくつもの弱学習器を作成するため, 弱学習器として計算量の少ない単純なものを使ったほうが費用対効果の面で優れることになります. どのような学習器がアンサンブル学習に向いているかについては, これからより詳しく掘り下げていきます.

なぜこのような方法で性能が上がるのでしょうか. バイアス・バリアンス理論の観点から言えば, アンサンブル学習はバリアンスを低下させる作用があるため, 性能が上がります. そのためもともとバリアンスの低い傾向のある学習アルゴリズムに適用してもあまり効果がないです. 一方で, 異なるタイプの学習アルゴリズムの併用することで効果を発揮します. また, 弱学習器の性能に大きな差がある場合も有効ではありません. これは, 弱学習器が真のモデルをそれぞれの方法で近似しているため, 精度の近い弱学習器どうしの平均をとることで, より真のモデルに近似できるということです. この原則に忠実なアルゴリズムの典型例が, 複数の決定木を使用するランダムフォレストで, 決定木は調整次第でいくらでもモデルの自由度を向上することができますが, そのぶん過学習しやすく, また単体でのバリアンスが比較的大きくなりやすいとされています.

10.1.7 ランダムフォレストとバギング

バギング (bagging) はブートストラップ集約 (Bootstrap AGGregatING) を意味します(Breiman 1996). データから無作為に観測点をいくつか抽出し, これを擬似的なデータとします. このような操作のことをブートストラップ法といい, こうして作成した擬似的なデータをブートストラップ標本と言います (Efron (1979) 本来のやり方とは少し異なりますが).

ブートストラップ標本を複数作成し, それぞれで弱学習器を作成し, それぞれの予測値を総合し, メタ学習器 (多くは単純な平均化) で最終的な予測値を決定します. 単純な仕組みなのですぐに使うことができ, その性質上並列処理をしやすいという利点があります. 一方で後述のスタッキングやブースティングはより複雑ですが, 工夫の余地があるため, より当てはまりの良いモデルを作れる可能性があります.

ランダムフォレスト (random forest) はバギングの一種とみなすことができます. ブートストラップ標本それぞれに対して決定木で学習器をつくり, 結果を多数決で決めます. ただしランダムフォレストのもう1つの工夫として, それぞれの決定木に用いる特徴量もランダムに選ぶことで過学習を防いでいます. ここでは, 決定木の説明した時と同じデータを使い, 木の深さを最大4とした7つの決定木でランダムフォレストを適用した結果を図 10.10に示します (わかりやすさのため, 特徴量のランダム選択はしていません). これを見ればわかるように, 決定木は同じパラメータでもかなり異なる分類境界を描きます. バイアス-バリアンス分解で説明するならば, 決定木はばらつき, つまりバリアンスの大きなアルゴリズムです. そこで, 複数の決定木の結果の平均をとることでバリアンスを低減させようというのが, ランダムフォレストというアルゴリズムのアイディアです.

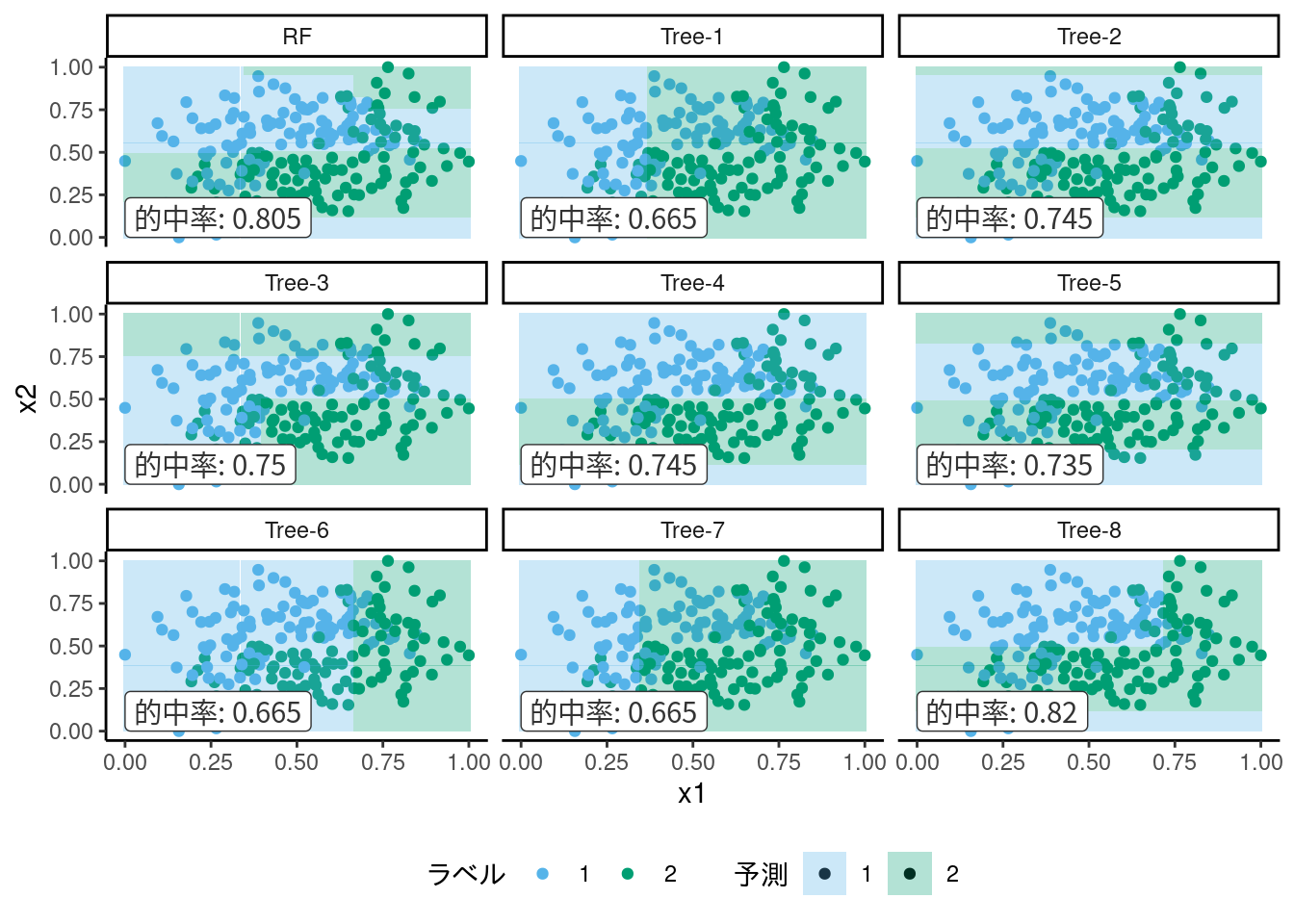
ランダムフォレストの各木の決定領域とメタ学習器の結果

図 10.10: ランダムフォレストの各木の決定領域とメタ学習器の結果

10.1.8 ブースティング

ブースティングもアンサンブル学習の一種ですが, それぞれ独立・並列して学習させるバギングと違い, それ以前の学習結果を反映して学習を繰り返すという再帰的な方法です. つまり, 1度学習した際に, 観測点のうち, 分類のうまくできないものに対して重み (重みベクトルとは別物です) \(w_{t}\) を与えます. 次の学習では, 損失関数は各観測点の重み平均となります. t 回目の学習で最小化する損失関数を \(L_{t}(\theta)\), 重みを \(w_{i,t}\) とすると, 以下のようになります.

\[\begin{align} L_{t}(\theta):=&\frac{\sum w_{i,t}l_{i}(\theta)}{\sum w_{i,t}} \tag{10.2} \end{align}\]

重みの大きい観測点は誤分類した場合の損失が多く見積もられるため, boosting の試行回数の進んだ学弱習器 はより分類の難しい観測点に適合しやすい可能性があります. しかし同時にそれは, 重みのない状態で正しく分類できた「簡単に分類できる観測点」が逆に誤分類しやすくなります. そこで, 最終結果ではなく, 繰り返しの途中で作られた \(t=1,2,\cdots\) 回目の学習器全ての予測値を元に最終結果を出力します.

これが最もシンプルなタイプのブースティングのアイディアです. 実際には様々な方法で複数のモデルに重み付けをするため, (10.2) 式がブースティング法の一般式というわけではありません. です. ブースティングは試行回数が多いほど損失が小さくなりますが, ある程度でやめないと過学習します. しかし, 数十-百回程度の反復でもかなり当てはまりの良い学習器が得られること, 使いやすいインターフェースの実装がオープンソースで複数公開されていることなどから, 比較的手軽に使うことができます (図10.11).

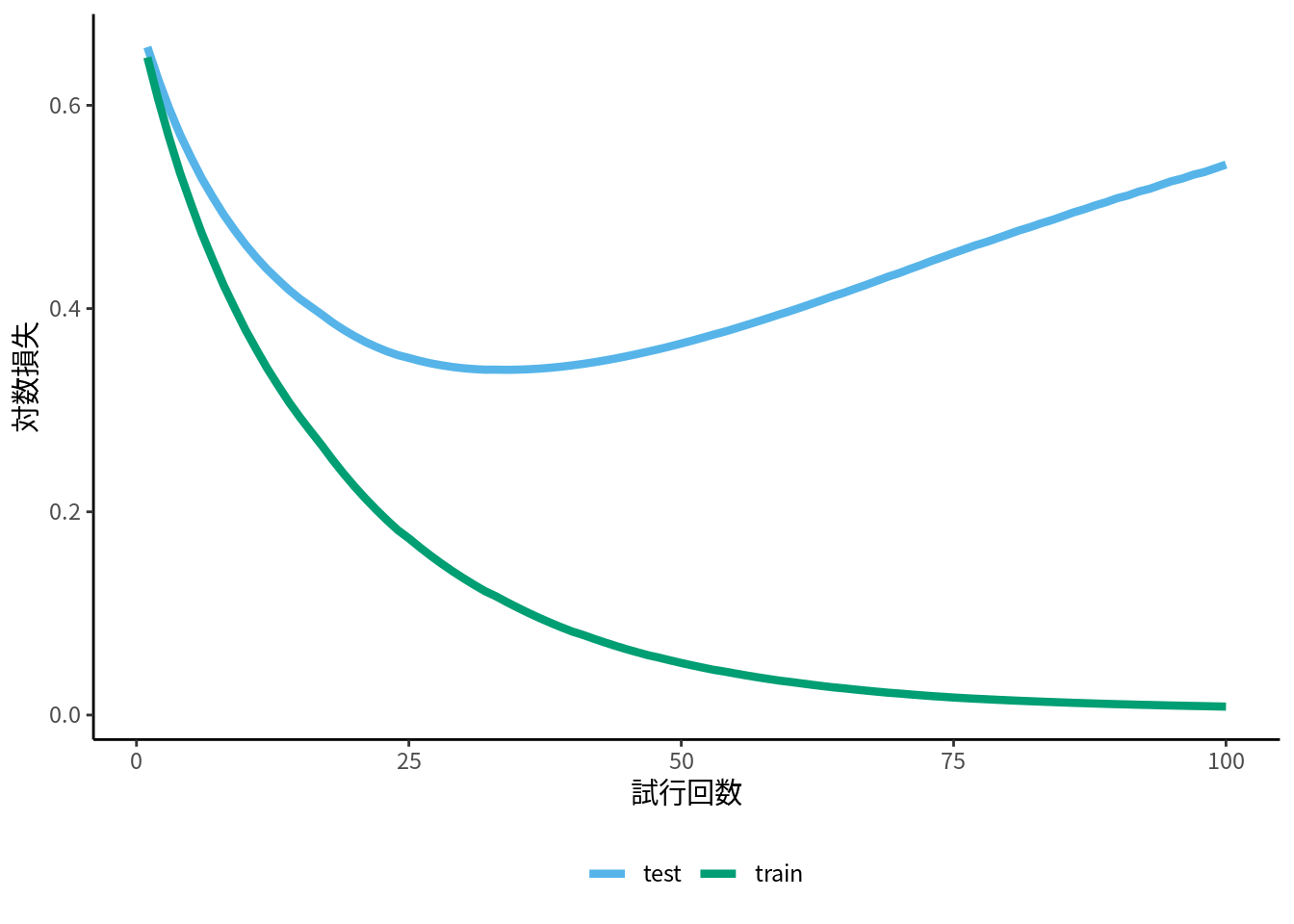
XGBoost の学習曲線の例, 適切な試行回数の相場はデータやハイパーパラメータ次第であることに注意

図 10.11: XGBoost の学習曲線の例, 適切な試行回数の相場はデータやハイパーパラメータ次第であることに注意

Adaboost は適応的 (adaptive) boosting の略で, 指数損失を利用した学習アルゴリズムです. 図 10.1 でわかるように, 指数損失はマージン \(m\) がマイナスのとき指数的に損失が増加する関数です. 二乗損失の説明を覚えていれば, 指数損失を使った学習は外れ値に弱いのではないか, と思うかもしれません. Adaboost は, 外れ値に対する感度の高い指数損失をもとに各観測点の重みを決定します. 弱学習器は決定木を使うことが多く, Adaboost tree と呼ばれます.

しかし, Adaboost も依然として実用上使いづらい弱点がいくつかあります.46 そのため, 重み付けとして1つ前の反復計算での1次・2次導関数を利用するタイプの, 勾配ブースティング と呼ばれるアルゴリズがより好まれます. 弱学習器にはやはり決定木がよく使われ, これは勾配ブースト決定木 (GBDT; gradient boost decision tree, あるいは単に GBT とも) と呼ばれます.

GBDT の実装は scikit-learn にも sklearn.ensemble.GradientBoostingClassifier や HistGradientBoostingRegressor というクラスがありますが, ブースティングを応用した実装プログラムとして, 最近開発された XGBoost (DMLC製) (Chen and Guestrin 2016), lightGBM (Microsoft製) (Ke et al. 2017), catboost (Яндекс製) (Prokhorenkova et al. 2018) などがよく用いられます (しかし今回のタスク的には, CatBoost は不向きかと思います.). GBDT は scikit-learn にも実装が存在しますが, 前述の XGBoost や Light GBM のほうが簡単な調整でできることが多く, またこれら計算が比較的高速なので人気があります. これらが便利であるのは, 純粋な Boosting 以外にもいろいろなアルゴリズムを利用して計算を工夫しているためです. それらは開発者らの論文に詳しく書かれています.

参考文献一覧

Albert, A., and J. A. Anderson. 1984. “On the Existence of Maximum Likelihood Estimates in Logistic Regression Models.” Biometrika 71 (1): 1–10. https://doi.org/10.1093/biomet/71.1.1.
Breiman, Leo. 1996. “Bagging Predictors.” Machine Learning 24 (2): 123–40. https://doi.org/10.1023/A:1018054314350.
Chen, Tianqi, and Carlos Guestrin. 2016. “XGBoost: A Scalable Tree Boosting System.” In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining - KDD ’16, 785–94. New York, New York, USA: ACM Press. https://doi.org/10.1145/2939672.2939785.
Efron, B. 1979. “Bootstrap Methods: Another Look at the Jackknife.” The Annals of Statistics 7 (1): 1–26. https://doi.org/10.1214/aos/1176344552.
Fan, Jianqing, and Runze Li. 2001. “Variable Selection via Nonconcave Penalized Likelihood and Its Oracle Properties.” Journal of the American Statistical Association 96 (456): 1348–60. https://doi.org/10.1198/016214501753382273.
Hastie, Trevor, Robert Tibshriani, and Jerome Friedman. 2009. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Second. Springer.
Ke, Guolin, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, and Tie-Yan Liu. 2017. “LightGBM: A Highly Efficient Gradient Boosting Decision Tree.” In Advances in Neural Information Processing Systems 30, edited by I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, and R. Garnett, 3146–54. Curran Associates, Inc.
Prokhorenkova, Liudmila, Gleb Gusev, Aleksandr Vorobev, Anna Veronika Dorogush, and Andrey Gulin. 2018. “CatBoost: Unbiased Boosting with Categorical Features.” In Proceedings of the Neural Information Processing Systems 2018, edited by S. Bengio, H. Wallach, H. Larochelle, K. Grauman, N. Cesa-Bianchi, and R. Garnett, 6639–49. Palais des Congrès de Montréal, Montréal Canada: Curran Associates, Inc.
Zou, Hui, and Trevor Hastie. 2005. “Regularization and Variable Selection via the Elastic Net.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 67 (2): 301–20. https://doi.org/10.1111/j.1467-9868.2005.00503.x.
富岡亮太. 2015. スパース性に基づく機械学習. 機械学習プロフェッショナルシリーズ. 東京: 講談社.
川野秀一, 松井秀俊, and 廣瀬慧, eds. 2018. スパース推定による統計モデリング. 6. 共立出版.

  1. 機械学習というより統計学の分野では, ロジスティック回帰など, 目的変数を0-1と定義することが多く, scikit-learn などでも 0, 1 の2値として扱われますが, 両者に本質的な違いはありません. \(\{-1, 1\}\) から \(\{0, 1\}\) へは, \(y^\prime = 2y - 1\) で容易に変換できます. 確率との対応を考えると \(\{0, 1\}\) のほうが直観的にわかりやすいですが, \(\{-1, 1\}\) ならば対称な式として表現できます.↩︎

  2. たとえば統計学でのロジスティック回帰は目的変数を0-1とし, \(0.5\) をしきい値にして分類するものと定義されることが多いですが, \(g(x)\) に定数項を加えることでしきい値をゼロに調整できるので, 両者に本質的な違いはなく, これ以降で導かれる結論はどちらにも当てはまります.↩︎

  3. ここでは分類モデルとして扱っていますが, ロジスティック回帰は回帰モデルともみなせます. ここでは慣例的な呼び方である「ロジスティック回帰」を使用しています.↩︎

  4. 分類なのに「回帰」と呼ぶのは不自然かもしれませんが, 統計学ではロジスティック回帰は連続変数の回帰モデルの拡張として考案されたため, 慣例でこう呼びます.↩︎

  5. このような場合は, 異常検知の文脈で1クラス分類問題と呼ばれています. これは1クラスの情報から, 各観測点が1クラスに属するかどうかを判定する学習です. 今回はそのような手法の出番はないと思われるので説明をしません.↩︎

  6. これは計算技術の問題ではありません. つまり, ニュートン法ではなく SGD で計算した場合, 計算することはできますが問題じたいは解決されていなことに注意してください.↩︎

  7. scikit-learn の LogisticRegression の正則化パラメータ C は, \(\lambda\) の逆数であることに注意してください.↩︎

  8. あるいは, ラグランジュ未定乗数法をご存知の方ならば, (10.1) が, 解がノルムの周上にあることを制約条件に課した条件付きの最小化問題とみなすことで, ここでいわんとしていることがわかるかと思います. ただしL1の場合は厳密にはラグランジュ未定乗数法で解くことはできません. スパース推定の最適化計算については, 富岡 (2015) が参考になります.↩︎

  9. ただし, L1正則化は「正しい」特徴量だけを選ぶ, というわけではありません. そのような性質はオラクル性と呼ばれ, L1正則化はオラクル性を持たないことが証明されています. オラクル性を持つ正則化項としてSACDなどが提案されています (Fan and Li 2001).↩︎

  10. この設定は一部のアルゴリズムでパラメータのオラクル推定を保証するために必須ですが, 予測モデルではパラメータの一致は必須ではありません. しかしどちらの場合でも, このように規格を統一することで問題の原因を見つけやすくすることができます.↩︎

  11. 実は「メタ学習」という用語は歴史的には, モデルの学習パターンに対するメタな学習方法のことを指します. 文脈に注意してください.↩︎

  12. あるいはモデル統合 (model integration) という用語もあります.↩︎

  13. Adaboost の問題や改善のヒントは Hastie, Tibshriani, and Friedman (2009) の10章が参考になります.↩︎