12.1 過学習とはなにか
ここまでで過学習という言葉を何度も使ってきましたが, 過学習とは具体的に何なのかの説明はしていませんでした. モデルの学習は与えられた訓練データで行いますが, 多くの機械学習の利用は訓練データ以外のデータ (補外データ) に対して予測に使いたいというのが動機で, 今回もそうです. 過 (剰) 学習 (overlearning) あるいは過剰適合 (overfitting) とは, 訓練データの当てはまりに対して補外データの当てはまりが良くないという現象を意味します. その逆は 過少学習 (underlearning) / 過小適合 (underfitting) と呼ばれます. しかしたいていは過少より過剰になることのほうが多いです.
過学習の発生する原因は確率的な要因です. これは個人的な意見ですが, 確率的な要因を次のように2つに大別して考えるとわかりやすいかもしれません.
- 観測データの偏り (ラベル・特徴量の分布シフト, 偏ったデータ抽出, 無限大の母集団を有限なデータで推定すること)
- 観測誤差(個々の値につきまとうランダムなノイズ)
この2つのうち (1) は, 単純に当てはめるデータと予測したいデータの特性が違うということです. 通常の方法では特性の違うデータ, 学習対象でない情報に対しても良好な当てはまりとなることはありません. この偏りの傾向が事前に具体的にわかっていれば補正する方法がありますが, 分からない場合はこの問題を解決することは難しいです. よって標準的な機械学習では, 訓練データと補外データの分布が同一であるということを暗黙の前提としています. 次に, (1) のような偏りがなかったとても, データには様々な理由で不確実さが含まれます. それはシステム誤差と呼ばれるものだったり, 計測機械の性能が絡むものだったり, そもそも完全なデータが取得できないということだったり, とにかくデータから得られる特徴量だけでは確定できない要因です. そして実務では, 特徴量では確定できない要因は必ずといっていいほど存在します. そのようなランダムな要因は特徴量で当てはめることは不適切なのですが, 確定的な部分と確率的な部分を分離することができないため, 不適切な当てはめが発生します. これが (2) の問題です. これらの対処法には, 既に説明したL1正則化などがあります. この観点では, 正則化によって訓練データの当てはまりこそ悪化しますが, 補外データへの当てはまりは正則化を使わない場合に比べて改善される場合があります. これは理論的な証明が可能ですが, ここでは一般的な理論解説は控え, Hastie, Tibshriani, and Friedman (2009) の提示したイメージだけを紹介します (図 12.1). 青い円の中心に真のモデルがあり, 真のモデルに近いものを学習によって作るのが目的です. しかし, ここで見落としてはならないのは, 単に真のモデルと距離が近い, というだけでは不十分ということです. モデルと真のモデルとのズレはバイアスと呼ばれ, 確かに小さいほうが望ましいのですが, バイアスの小ささに加え, ばらつき, つまりバリアンスの小ささも重要になります.この図では黄色い円でモデルのバリアンスの大きさが表現されています. そして学習したモデルと真のモデルの近さは, 中心点どうしの距離ではなく, 真のモデルと, 学習したモデルのバリアンス円の最も遠い点の距離で表わされます. 正則化を用いない場合はバイアスを小さくすることができますが, バリアンスを考慮しないため大きくなりがちです. 正則化という一見すると「よけいな」制約をモデルを加えることでデータにぴったりと当てはまらなくなり, 当てはまりが悪くなっている (図中の “estimation bias”) ように見えますが, バリアンスが小さくなるため実際には真のモデルにむしろ近づける可能性があるというのがこの図の意味するところです.
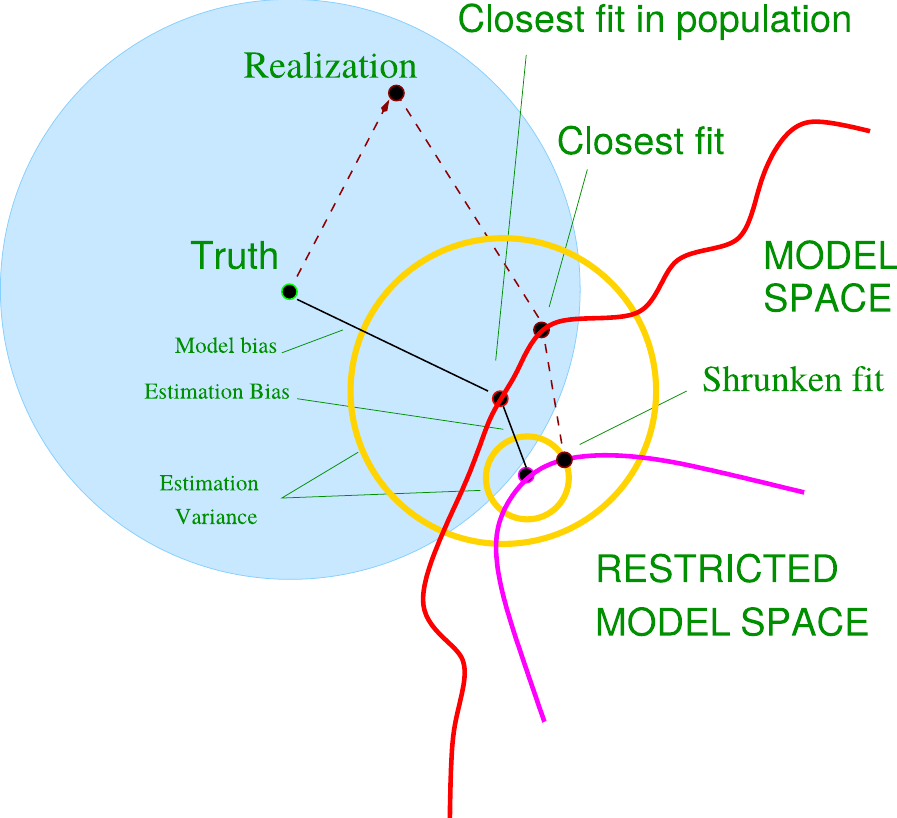
図 12.1: Hastie, Tibshriani, and Friedman (2009), 225ページより
これはバイアス・バリアンス分解定理の視覚的な説明です. 数式を使って確認してみましょう. ここでは, 簡単のために回帰問題の場合で考えます. \(y\) の予測モデル \(\hat{y} = f(x)\) が用意できたとします. すると, \(y - \hat{y}\) がモデルと実際の値の誤差であり, これが小さいほうが予測として望ましいはずです. ということは単純に \(y - f(x)\) をデータ全体で計算すれば良いと思われるかもしれません. 実際, 回帰モデルでは平均二乗誤差 (MSE) やその平方根である RMSE がモデルの当てはまりの指標としてよく計算されます. しかし既に挙げたようにデータには2種類の不確実性があります. 取得できるのは一部のデータのみで, 未来のデータなどは絶対に取得できませんし, 観測するデータ自体にも様々な原因でノイズが含まれている可能性があります. よって, 取得したデータの範囲内での計算ではなく, 誤差の理論上の期待値 (汎化誤差) を考える必要があります. 平均二乗誤差にならい, \((y - \hat{y})^2\) に対する期待値 \(\mathrm{E}(y - \hat{y})^2\) で見た誤差を考えます. この期待値は, 以下のように3つの項に分解できます48.
\[\begin{align} \mathrm{E}(y-\hat{y})^2 =& (\mathrm{E}[y] - \mathrm{E}[\hat{y}])^2 + \mathrm{E}\left[(\hat{y} - \mathrm{E}[\hat{y}])^2\right] + \mathrm{E}\left[(y - \mathrm{E}[y])^2\right]\\ =& \mathit{bias}^2 + \mathit{variance} + \sigma_y^2 \end{align}\]
右辺は第1項から順に, 2乗バイアス, バリアンス, 雑音 (ノイズ) または観測誤差と呼ばれます. 最後の雑音は計測の誤差や現象そのもののランダムさに由来するため機械学習では削減できない要因ですが, 2乗バイアスとバリアンスはモデルに依存します. バイアスは \(y\) からランダムさを除いた \(\mathrm{E}y\) との差を表しています. つまり, \(y\) からノイズを除いた「真の値」とのずれの大きさを表します. 一方で, バリアンスはモデルの予測値についての分散を表しています49. よって, 2乗バイアス項が図 12.1 の Truth から closest fit in population の距離である model bias に対応し, バリアンスが黄色い円の半径 (estimation variance) に対応します. ただし,この式では予測モデル \(\hat{y} = f(x)\) を固定していることに注意してください. 実際には予測モデルは訓練データによって作られ, 訓練データもまた「データ全体」からサンプリングされたものであるため, ここから生じる \(\hat{y}\)の確率的な誤差は, \(\mathrm{E}\hat{y}\)とは正確には異なることを考慮する必要もあります (予測モデルは未来のデータに対しての予測が目的なので, まず一致しません).
この定理から興味深い事実が得られます. まず, 平均二乗誤差 (MSE) や対数損失といった目的関数はモデルの誤差の一部, バイアスの部分だけを間接的に評価していることがわかります. さらに, 予測値はバイアスにもバリアンスにも影響します. よって, 最小二乗法やロジスティック回帰をそのまま適用して得た予測値は汎化誤差全体を最小化するとは限らず, むしろ正則化によってこれらのアルゴリズムの最適化に制約を与えたほうが, かえって汎化誤差を小さくできる可能性があるということです50.
そして, 上記の説明では, 真のモデルが存在するという前提であることに注意してください. 現実の問題を扱う我々が「真のモデル」を特定する, あるいは実在するかを知ることは究極的には難しく,51 上記の説明は一見して, 真のモデルがなんであるか言及していないように見えますが, 実際には真のモデルが \(y = f(x) + \varepsilon\) という式, つまり確定的な関数 \(f(x)\) と確率的な誤差 \(\varepsilon\) の和であるという「仮定」を含んでいます. ここまでの説明では問題を切り分けるためにバイアスとバリアンスに限定して話しましたが, 実際にはそれに加え, モデルの特定化の誤りについても考慮する必要があります. 例えば, (1) の問題で言えば, 訓練データとテストデータとで特徴量の傾向が全く変わらないと想定することも, 一種のモデルの仮定です. しかし現実にはそうである保証はありません (特に今回のタスクでは, そう考えるとうまく行かないことが多いです).
参考文献一覧
式展開は Hastie, Tibshriani, and Friedman (2009) の7章や 中川 (2015) の4章を参考にしてください.↩︎
モデルの予測値の分散が何を意味するのかというと, モデルの予測値は学習によって決まります. つまり, 訓練データがランダムに選ばれたとすると, 得られるモデルもそのランダム性の影響を受けます. つまり, バリアンスは学習アルゴリズムがどれだけデータの影響を受けやすいか, 過学習しやすいかを表しているとも言えます. 複雑な関数を近似できるモデルほどデータに適応しやすいので, 例えば既に紹介した決定木のようなモデルはバリアンスが大きくなりがちであると言えます.↩︎
機械学習の正則化は, 経験ベイズ法における事前分布に対応するものとみなすことができます. 事前分布の有用さを示す有名な具体例として James-Stein の推定量と呼ばれる問題があります. この問題について, たとえば 伊庭 (2018) の説明が分かりやすいでしょう.↩︎
この考え方が正しいのかどうかは突き詰めると哲学的な議論になります.↩︎