9.2 事後診断と改善のヒント
最適化とは1つの指標を最大 or 最小にすることですが, 単一の指標だけを見ていてもはわからないことも多いです. それがなぜ良かったのか(悪かったのか), どうすれば改善できるか, という問いは総当りで良い指標を求めているだけでは解決できません. 結果に対する「反省」が必要です.
モデルが単に良い指標を示しているかだけでなく, 適切に使用されているかどうかを確認することを事後診断 (posterior diagnosis) と言います (この語はあんまり広く普及してない気もするので私の造語という扱いでもいいです). CTR 予測では, 単に当てはまりの良いモデルであるだけでなく, 予測として使えるものかどうかを見ることが必要です. 原因を見つけるのはルーチンワーク化するのが難しく, あらゆる異常を見つける方法はありませんが, いくつか有用な確認方法を以降に紹介します.
9.2.1 予測確率のユニークカウント
予測 CTR は広告のプライシング計算に必要なので, もしほとんどが同じ値である場合, 使えるか疑わしいです. そのため, 当てはまりがよくても予測確率のユニークカウントを確認してください. 単に学習方法が不適切だった場合は検証データの当てはまりが極端に悪くなるため気づきやすいですが, それがなぜかを知るためにはこのような確認で原因がわかることがあります. 決めつけは禁物ですが, ユニークカウントが極端に小さい場合, 入力データまたは前処理したデータに問題があるため学習アルゴリズムがうまくはたらかないことが多いです. そしてその場合は NE の値など他のところにも影響が見られます.
9.2.2 予測確率のヒストグラム
予測確率のヒストグラムを作成すると, ユニークカウントより多くの情報が得られます. ユニークカウントと違い, 予測確率のボリュームゾーンがどこにあるのかが分かります. 訓練データの当てはまりに対して検証データの当てはまりがあまり良くないとき, 訓練データと検証データそれぞれでヒストグラムを描いて比較すると, それが過学習によるものなのか, それ以外の要因によるものかを知るヒントになります. もし分布の形状やピークの位置が全く異なっていたのなら, 過学習というより正負例の変化や特徴量の分布が変わっているのが原因である可能性があります. 特徴量全ての分布を確認するのは大変なので, まず予測確率で簡易的に確認するというのは有効です(図 9.1).
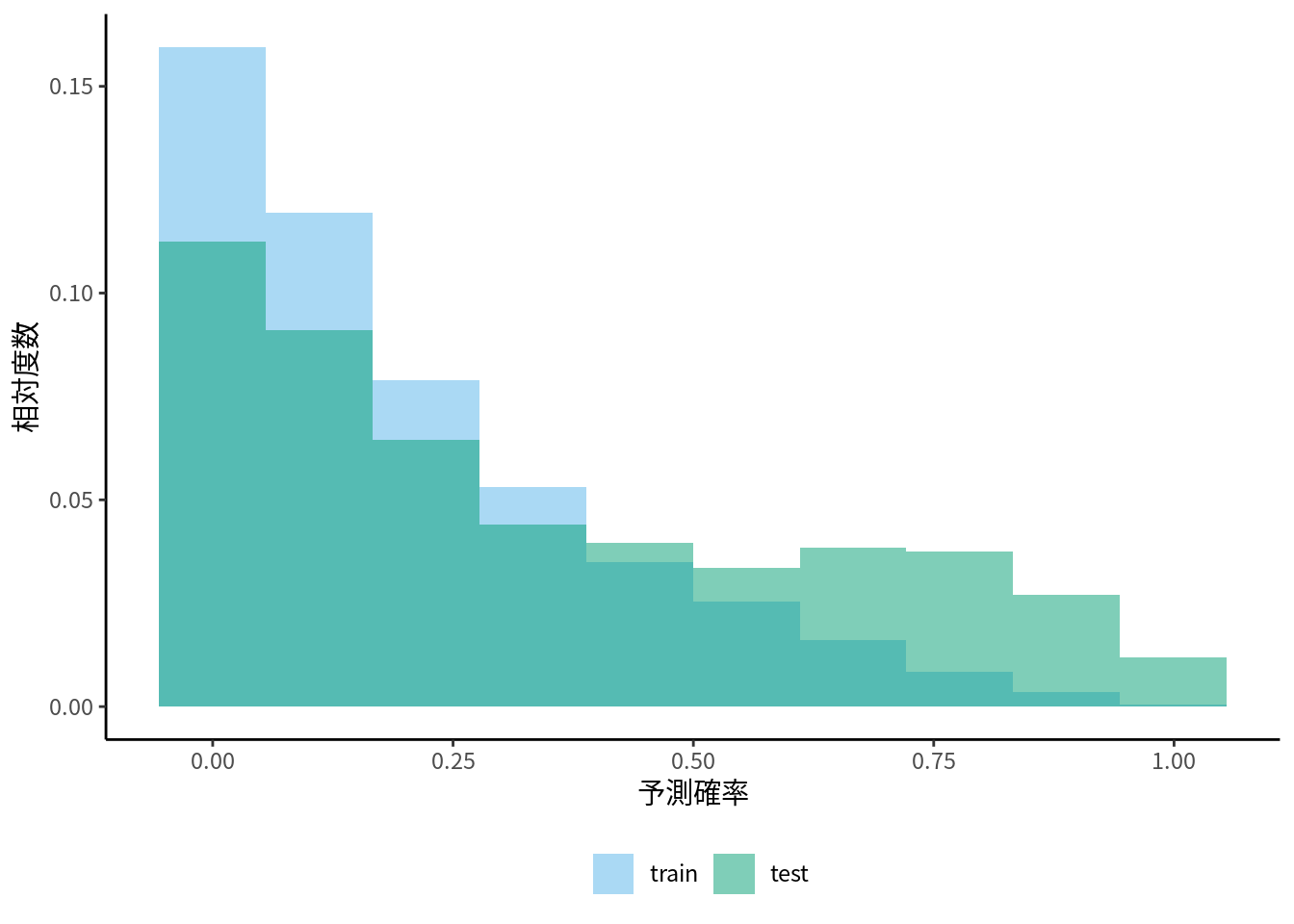
図 9.1: 予測確率のヒストグラム
たとえばピークが複数ある場合, 特定の特徴量の値を持つ一部のデータに原因があるかもしれません. そのピークに含まれるデータだけを取り出して, 傾向を確認してみると何かわかるかもしれません. これには 7 章で紹介したグラフ作成の方法が役に立つことでしょう.
データごとに正負例の割合が大きく違うことをクラスバランス変化, 特徴量の分布が大きく違うことを共変量シフトと呼びます(杉山 et al. 2014). 学習アルゴリズムの多くは訓練データもテストデータも同じ分布に由来するものであるという前提なので, このような状況を想定した最適化はできません. これらに対しては分布の変化を考慮した学習アルゴリズムが考案されていますが, 共変量シフトやクラスバランス変化の影響が少ないように特徴量やクラスラベルを変換する, という方法もときには使えるかもしれません.
9.2.3 複数種類の評価指標の比較
多くの場合, 評価指標の特性は似たりよったに感じられるかもしれませんが, 全く同じということはありません. 例えば的中率とF値, そして混同行列を確認すると, 的中率は高いが, F値はあまり高くない, そして混同行列を見ると, 一部のセルだけ値が大きい. このような場合は, ラベルの不均衡が原因で見かけほど当てはまりがよくないと疑えます.
今回のCTR予測ではこれらの指標はあまり意味がないため, 予測確率の当てはまりの指標として対数損失かNEを使用します. しかし, それ以外の指標が全く使えないというわけではありません. Brier スコア (Brier 1950) は回帰モデルを評価する平均二乗誤差 (MSE) をそのままラベルと予測確率に当てはめたものです. 小さいほうが良いというのは同じですが, 二乗誤差で評価しているため対数に比べて敏感に変換しません. よって, 当てはまりが良い/悪い原因に一部の外れ値が寄与しているのかどうかを知るヒントになります. 同様の理由で, 平均絶対誤差 (MAE) と併せて比較するのも良いかもしれません. しかし, 分類問題では0から1の値しか取らないため, スケール調整に注意してください (図 9.2).
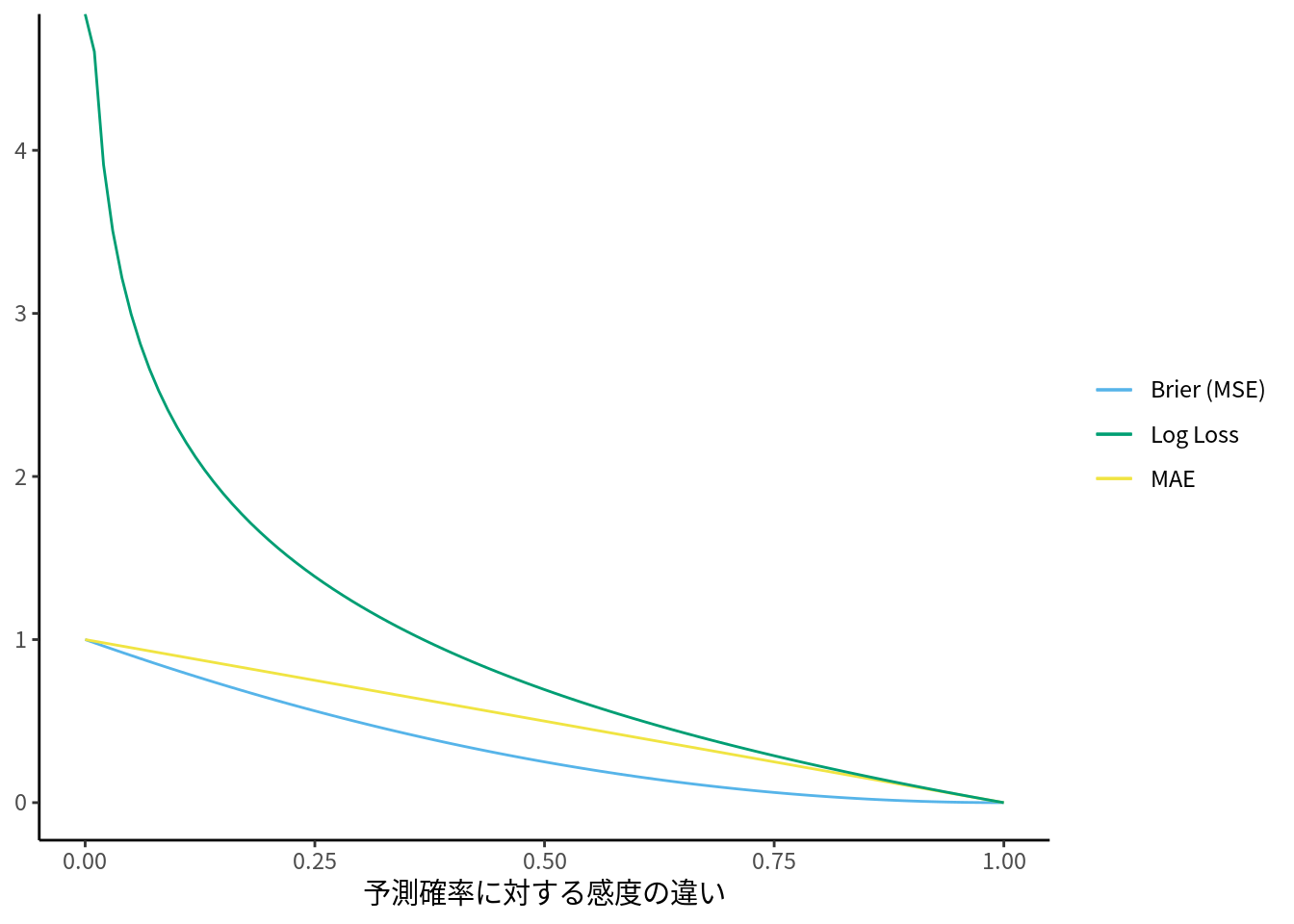
図 9.2: y=1 に対する予測確率の誤差の大きさ
分類モデルでは ROC曲線の下側の面積, いわゆる AUC-ROC もよく使われます. AUC は0から1の間を取り, 1に近いほど「良いモデル」であるという指標であるため, 一見して分かりやすい指標です. しかし AUC はいわゆる順序統計量の一種で, 予測確率の絶対値ではなく予測値どうしの相対的な大小関係を評価するものです. よって, CTRの予測確率の評価としては不十分です30. しかしながら, 直接の評価には使えなくとも活用の余地はあります. AUC は確率の絶対的な大きさを評価することはできませんが, モデルが正例と負例の場合でどれだけ予測値に開きがあるかを意味する判別性能 (descrimination) を評価することに使えます. 優先すべきは予測確率の絶対値ですが, NEが良い割に AUC が低いのでよく確認してみるとどのデータに対しても同じような値を返している, さらに詳しく調べてみるとプログラムにバグがあった, ということも実際に私が体験したことです.
AUC は 0-1 の範囲で表されるため, 一見してわかりやすく, 広く使われています. しかし, AUC での評価が良いことが, 分類モデルとしてどう好ましいのかまで説明している人はあまり見かけません. 様々な評価指標のどれが取り組んでいる問題に適しているのか, よく考えて使いましょう.
9.2.4 分類モデルの残差診断
回帰モデルでは, 目的変数 \(y_i\) と予測値の差を残差 (residuals) と呼び, その分布の傾向を確認することがあります. 例えば以下のような線型回帰モデルを考えます.
\[ y_i = \beta_0 + \beta_1 x_{1, i} + \cdots + \beta_Kx_{K,i} + \varepsilon_i \]
このモデルがデータの分布の性質をうまくとらえ, よく当てはまっているなら誤差項 \(\varepsilon_i\) は残差に対応するはずです. その場合, 誤差項は (漸近的に) 平均がゼロの正規分布になるはずなので, ヒストグラムやQ-Qプロットを描くなどして残差が正規分布と同じ性質を持つか調べることで, 対数損失やAUCのような当てはまりの良さの数値以外の観点でもモデルの評価ができます.
もし当てはまりが悪い場合, 残差の分布の偏りから, モデルの改善方法のヒントが見つかることがあります. 例えば分布が非対称なべき分布のような形ならば対数変換で改善されるかもしれませんし, 分布のピークから外れた位置で不自然に突き出た箇所があるなら, 特徴量を追加することで自然な分布になるかもしれません.
少しづつモデルの設定や特徴量を調整するたびに残差ヒストグラムがきれいな分布になっているか確認する, というようなアプローチは, 当てはまりを良くする上である程度は有効です. しかし, 残差診断はもともとモデルの仮定がデータと矛盾していないかを確認するために考案されたものであり, モデルの予測性能を最適化するための方法ではありません. つまり, やりすぎは単なる訓練/テストデータへの過学習にしかなりません. 目先の分布を調整することにとらわれず, その不自然な残差がなぜ起こっているのかというメカニズムを考え, 過学習に陥らない改善方法はなにか, ということを意識すれば, より効果的かもしれません.
分類モデルの場合, ラベル \(y_i\) は2値しかないため, 回帰モデルと同じように残差を求めても4通りの値しか現れません.31 そのため, 回帰モデルの残差のような情報を分類モデルで得るための方法が複数提案されています.
9.2.4.1 応答残差
まず, 単純に 0, 1 のラベルから予測確率を引いたものを使う方法があります. これは応答残差 (response residuals) と呼ばれます.
\[ r_i^{(\mathit{Response})}:= y_i - \hat{p}_i \]
9.2.4.2 ピアソン残差
標準化のように, 応答残差をさらに予測値の標準偏差で割ったものはピアソン (Pearson) 残差と呼ばれます.
\[ r_i^{(\mathit{Pearson})}:= \frac{y_i - \hat{p}_i}{\sqrt{\mathrm{V}(\hat{p}_i)}} \]
ピアソン残差は一定の条件のもとで, 標準正規分布に従います.
9.2.4.3 逸脱度残差
これは一般化線形モデル (GLM) の逸脱度 (deviance, デビアンス) に基づいた, 逸脱度残差という指標です.
\[\begin{align} r_i^{(\mathit{Deviance})} := & \mathit{sign}(y_i -\hat{p}_i)\sqrt{(d_i)},\\ d_i = & -2 * (l_i(y_i, \hat{y_i}) - l_i(y_i, \tilde{y}_i)) \end{align}\]
\(\mathit{sign}()\) はカッコ内の値の符号を意味します. つまり \(y_i -\hat{p}_i \geq 0\) なら \(+1\), \(y_i -\hat{p}_i < 0\) なら \(-1\) となります. \(d_i\) は単位逸脱度 (unit deviance, casewise deviance) と呼ばれます. \(l_i(y_i, \hat{y_i})\), \(l_i(y_i, \tilde{y}_i)\) はそれぞれ, 観測点 \(i\) に対応する対数損失と, このモデルとは別に, \(y_i\) が必ず的中するように作ったモデル (フルモデル) の対数損失 (交差エントロピー) です.
これは一見すると回帰モデルの残差と異なるため, 意味が分かりづらいかもしれません. まず, 必ず予測が的中するモデルなど作れるのか, という疑問があると思います. 結論から言うと, 観測点の数だけ特徴量のあるロジスティック回帰モデルなどを使えば簡単に作ることができます. このようにして作られたフルモデルの予測が完全に一致するのは訓練モデル内だけであり, それ以外のデータの予測に対しては全く実用的なモデルではありません. しかし, 訓練データ内であれば, ラベルが的中した場合の損失とそうでない場合の損失の差を知ることができます. よって, データ全体についてこの差を取った逸脱度32 という指標は, 架空のモデルをベンチマークの比較対象としている NE と発想が似ています.
このようにして求めた逸脱度の平方根を取ると, フルモデルに対して正負どちらの方向にズレがあるのかわからなくなります. そこで最後に \(\mathit{sign}(y_i -\hat{p}_i)\) で符号を付けます. これが逸脱度残差です. これら3つ以外にも残差の定義は存在しますが, ここでは紹介を省略します.
応答残差とピアソン残差は回帰モデルのアイディアをそのまま転用したような形でありわかりやすいですが, 逸脱度残差の定義は複雑です. これは統計的に便利な性質を得るためのアイディアに基づいていますが, 単にグラフに残差をプロットする程度であればあまり変わらないことが多いです.
ピアソン残差や逸脱度残差は, 理想的な条件では正規分布に従うため, 回帰モデルでの残差診断と同様に良し悪しを見分けやすいです. しかし, ラベルが2通りしかないため, 一般的な傾向として,
- 残差の分布にはあまり多様性がなく, 得られる情報が少ない
- ゼロ付近の値が欠けた, 双峰型の分布になることがある
という問題があります.
数種類の異なる特性の乱数データを用意しました. それぞれ特徴量は2つだけです. それぞれの散布図は図9.3のようになり, 対応する残差ヒストグラムは図9.4です. “Normal” は中心をずらした2つの正規分布で作成した乱数データで, ロジスティック回帰で比較的あつかいやすいデータです. “Imbalanced” はラベルの比率が 95:5 と偏りがあるデータです. “Spiral” は2つのクラスの分布が互いに入り組んだデータで, ロジスティック回帰での分類がやや難しいです.33 “Spiral & Imbalanced” は “Spiral” なデータのラベル比率を偏らせたものです. 図9.4を見ると, ここまでの説明から予想できる通り, 単にラベルとの差を取っただけの残差 (“Label”) は値に多様性がなく, わかることは少ないです. 残りの3種類は似たような形状ですが, それよりも Spiral や Imbalanced などデータの種類によっては独特の形状になったり, やはり多様性がなくなったりします. よって, 線型回帰モデルと比べてどう見るべきかが変わってきます.
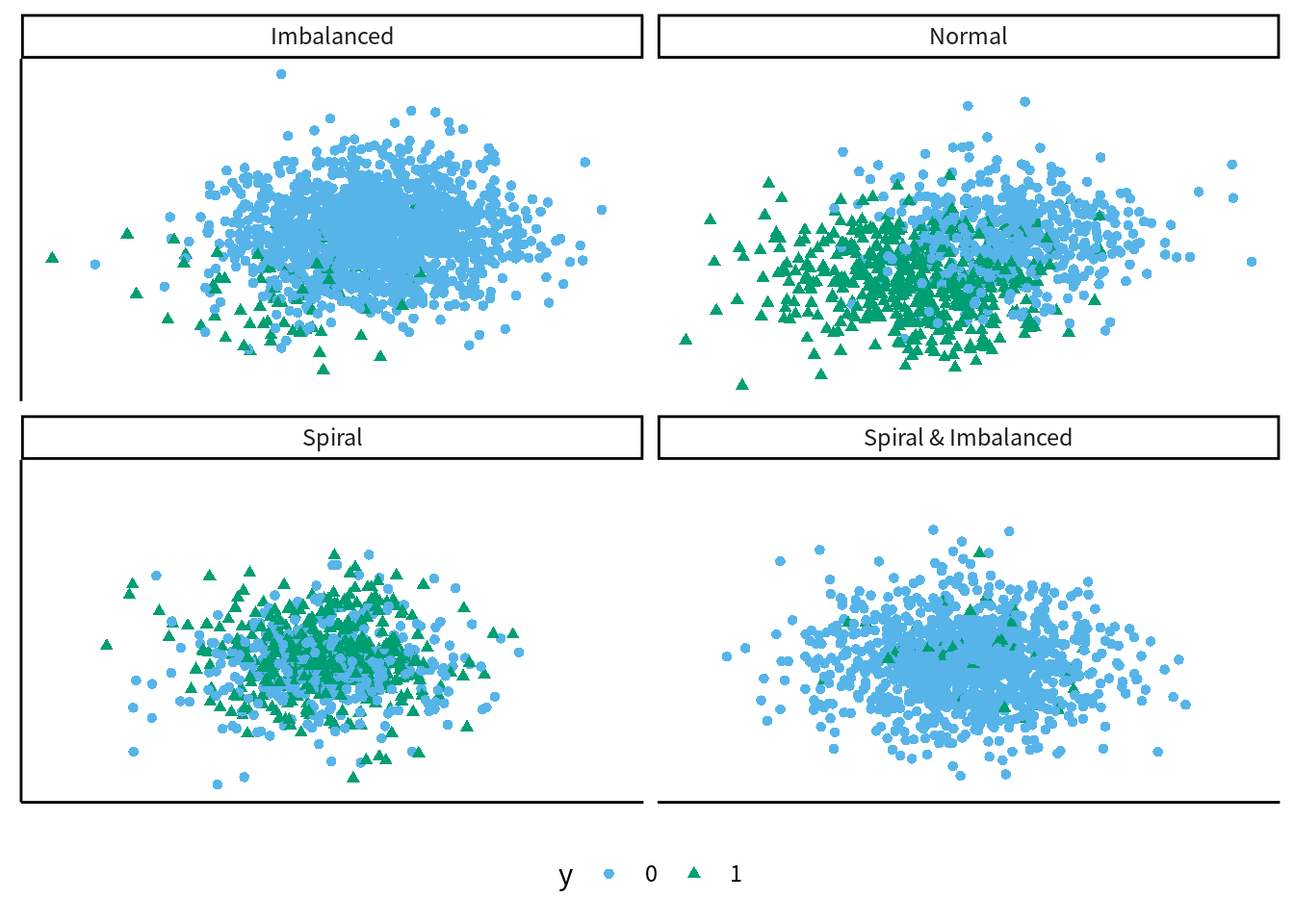
図 9.3: 訓練データの散布図
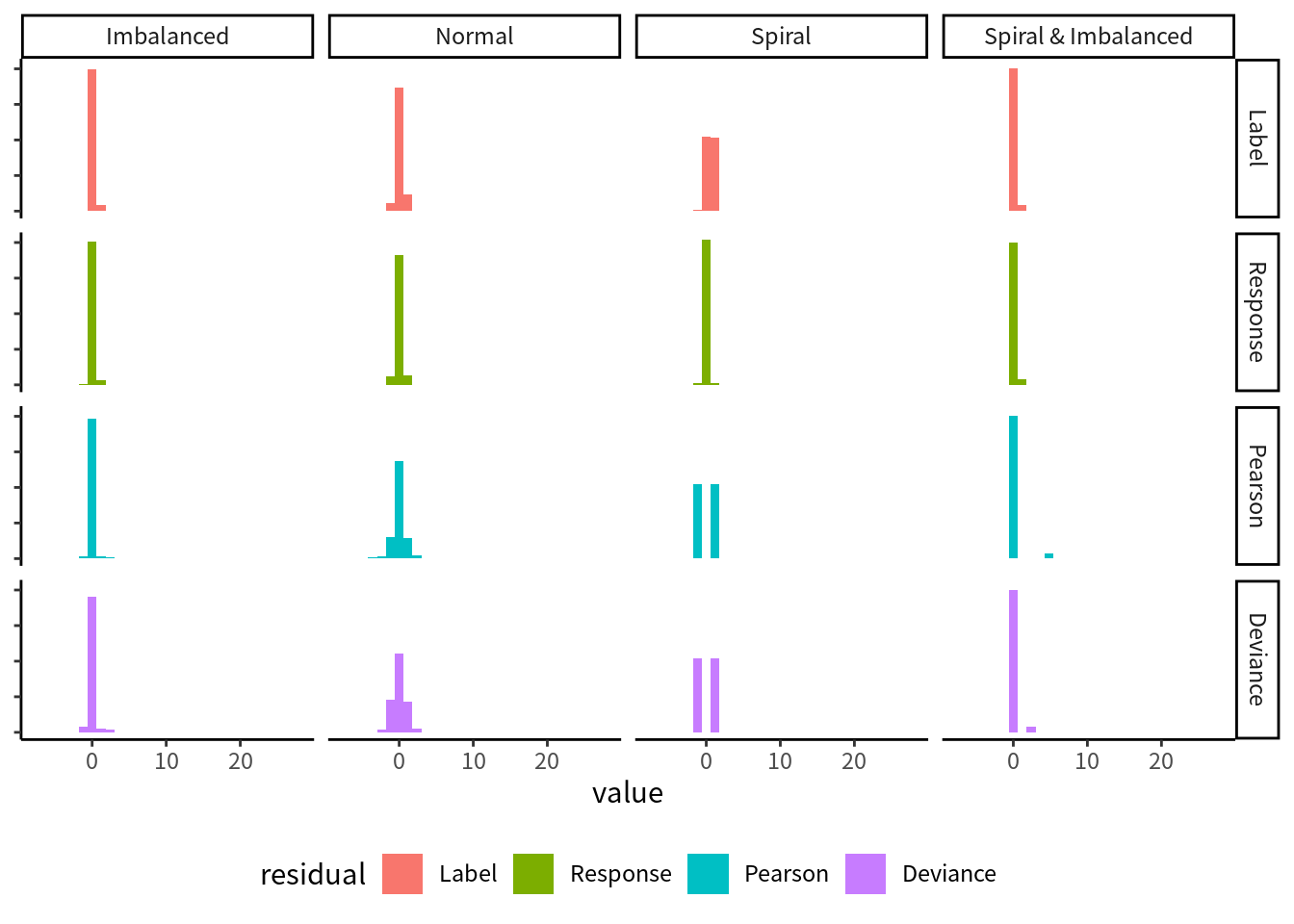
図 9.4: 異なるデータに対するロジスティック回帰を, 異なる定義の残差ヒストグラムで評価した場合
本稿では GLM や逸脱度については説明しないため, これらの概念についてより詳しく知りたい場合は 久保 (2012) などを参考にしてください. ただし, この教科書には逸脱度残差についての説明がありません. 私の知る限りでは, 逸脱度残差および分類モデルの残差診断に詳しい日本語の資料は (私の知る限り) ありません. 英語であれば Pierce and Schafer (1986), Davison and Snell (1991), Davison and Tsai (1992), Collett (2003) などがあります. ただし, これらは本稿のような機械学習による予測をテーマとして書かれた本でないことに注意してください. 加えて, これらは古いので個人で入手・購入するのが難しいかもしれません.
9.2.5 時系列データの残差診断
長い期間にわたる時系列データを扱う場合, 変数の変化に周期的な規則性が見られることが多いです. このような場合, 残差そのもののヒストグラムではなく, 残差の自己相関係数のプロット (コレログラム) を描画することも1つの手段です.
以前投稿した以下の記事は, 厳密でも網羅的な方法でもありませんが, 時系列データの性質を見つけ, どうすればモデルの改善につながるかの簡単なチュートリアルとして書きました.