13.2 数値変数の分布を変える
数値変数の分布が対称でない場合, 冪分布であることがよくあります. 冪分布は最も単純なケースでは対数変換によって対称分布に置き換えられます. もし厳密に冪分布でない, つまりゼロが含まれる分布に対してはログプラス1変換が有効です. と言っても文字通り1を足してから対数変換するだけですが.
対数変換を拡張したものとして, Box-Cox 変換 が古くから知られていおり, より柔軟に正規分布らしい形に変換できます. 以下のような変換式です.
\[\begin{align} x^\prime:= & \begin{cases} \frac{x^{\lambda}-1}{\lambda} & \text{if }\lambda\neq0,x>0\\ \ln(x) & \text{if }\lambda=0, x>0 \end{cases}\end{align}\]
\(\lambda\) は変換に必要なパラメータで, 変換後の値が正規分布に最も近くなるよう, 最尤推定で決定します.
さらに, ゼロやマイナスの値でも変換できるようにしたものに, Yeo-Johnson 変換 (Yeo 2000) と逆双曲正弦 (IHS) 変換 (Burbidge, Magee, and Robb 1988) があります. 式が Box-Cox変換より複雑になっています
YJ変換は以下で定義されます.
\[\begin{align} x^\prime:= & \begin{cases} \frac{(x+1)^{\lambda}-1}{\lambda} & \text{if }\lambda\neq0,x\geq0\\ -\frac{(x+1)^{2-\lambda}-1}{2-\lambda} & \text{if }\lambda\neq2,x<0\\ \mathrm{sign}(x)\ln(\left|x\right|+1) & \text{otherwise} \end{cases}\end{align}\]
IHS変換は以下で定義されます.
\[\begin{align} f(x):= & \theta\mathrm{arsinh}(\theta x)\\ = & \theta\ln(\theta x+\sqrt{\theta^{2}x^{2}+1}) \end{align}\]
Box-Cox 変換と Yeo-Johnson 変換は冪変換というカテゴリでくくることができるため, ver. 0.23 以降の scikit-learn では PowerTransformer というクラスで使用できます.
しかし, 数値変数でもゼロの頻度が非常に多いタイプの分布はべき変換をしても良い形になりづらいです. あえて特定の区間ごとに区切り, カテゴリカル変数に置き換えるビニング (binning) が有効かもしれません.
\((0, 1)\) の範囲にしか値がない場合, あえて \((-\infty, \infty)\) の範囲に拡張するとよいこともあります. ロジット変換ならば可能です.
\[\begin{align} x^\prime:= & \ln\left(\frac{x}{1-x}\right) \end{align}\]
ロジット変換の逆はロジスティック変換です (逆ロジット変換とも呼ばれます).
\[\begin{align} f(x):= & \frac{\mathrm{e}^{x}}{1+\mathrm{e}^{x}} \end{align}\]
これらの変換の違いを見てみましょう. 例として, 自由度5のカイ二乗分布に基づく乱数を生データとして, 各種の変換後と分布を比較したのが図13.1です. ロジスティックと IHS 以外はあまり変わらないように見えます.
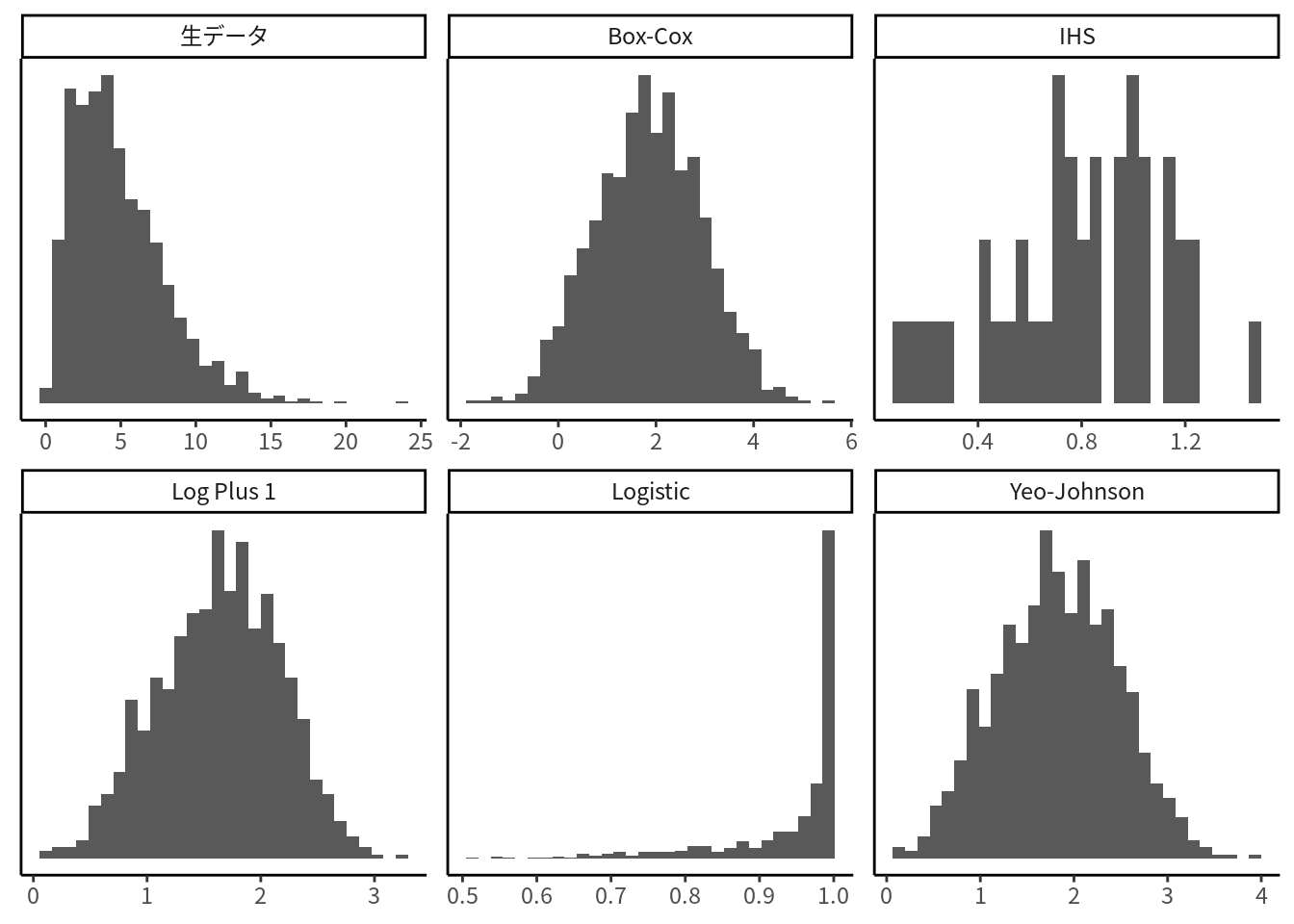
図 13.1: 生データと各種変換後の分布
ロジスティック変換は非対称な分布を想定した変換でないことは明らかですが, IHS 変換もややいびつな形になっています. これは値の一部が変換に失敗しているためです. IHS変換は正負両方の値をとり, かつ「偏った」分布では有効ですが, 今回のような負値のない分布ではうまくいかないことが多いです.